Kose Dekhi 5.3 Class 9 Solution রৈখিক সহসমীকরণ

প্রিয় ছাত্র ছাত্রী তোমাদের প্রয়োজনমত সব প্রশ্নের উত্তর দেওয়ার জন্য আমরা এই estudypoint ওয়েবসাইট বানিয়েছি। আজকের এই পোস্টে আমরা মধ্য শিক্ষা পর্ষদের নবম শ্রেণীর রৈখিক সহসমীকরণ: Kose Dekhi 5.3 Class 9 এই চ্যাপ্টারের গণিতের সম্পূর্ণ উত্তর দিয়েছি। যদি তোমাদের আরো ও গণিতের সমাধানের প্রয়োজন হয় তাহলে আমাদের এই ওয়েবসাইটের কমেন্ট বক্সে লিখে জানাবে। আমরা চেষ্টা করবো যত তাড়াতাড়ি তোমাদের প্রশ্নের উত্তর দিতে পারি।

Kose Dekhi 5.3 Class 9 Solution

1 . নিচের দুই চল বিশিষ্ট এক্ঘাত সমিকরনগুলি অপ্নয়ন পদ্ধতিতে সমাধান কর ও লেখচিত্রের সাহায্য সমাধান যাচাই কর।

(a) 8x + 5y – 11 = 0 , 3x – 4y – 10 = 0

8x + 5y – 11 = 0

8x + 5y = 11 …………….(i)

3x – 4y – 10 = 0

3x – 4y = 10 …………….(ii)

(i) সমীকরণকে 4 দিয়ে ও (ii) সমীকরণকে 5 দিয়ে গুন করে y চলকে অপনয়ন করে পাই,

32x + 20y = 44

15x – 20y = 50
__________________
47x = 94
x = 2

(i) নং সমীকরণে x = 2 বসিয়ে পায়

8x + 5y = 11

বা, 8 $\times$ 2 + 5y = 11

বা, 16 + 5y = 11

বা, 5y = 11 – 16

বা, 5y = – 5

বা, y = -1

(b) 2x + 3y – 7 = 0 , 3x + 2y – 8 = 0

2x + 3y – 7 = 0

2x + 3y = 7………..(i)

3x + 2y – 8 = 0

3x + 2y = 8…………(ii)

(i) নং সমীকরণকে 2 দিয়ে ও (ii) নং সমীকরণকে 3 দিয়ে গুন করে y চলকে অপনয়ন করে পায়,

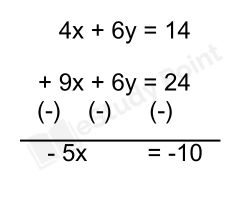
x = 2

(i) নং সমীকরণে x = 2 বসিয়ে পায়

2x + 3y = 7

বা, 2 $\times$ 2 + 3y = 7

বা, 4 + 3y = 7

বা, 3y = 3

বা, y= 1

2. 7x – 5y + 2 = 0 সমীকরণকে কত দিয়ে গুণ করে 2x + 15y + 3 = 0 সমীকরণের সঙ্গে যোগ করব যাতে y চলটিকে অপনিত করতে পারি ।

7x-5y+2 = 0 ………..(i)

2x+15y+3 = 0 ……….(ii)

5 এবং 15 এর লসাগু 15 অর্থাৎ y –কে অপনীত করতে গেলে (i) নং সমীকরণকে 3 দ্বারা গুণ করতে হবে ।

4. নীচের দুইচল বিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি ।

(i) 3x + 2y = 6 , 2x – 3y = 17

3x + 2y = 6 …………….(i)

2x – 3y = 17 …………….(ii)

(i) নং সমীকরণকে 3 দিয়ে ও (ii) নং সমীকরণকে 2 দিয়ে গুন করে y চলকে অপনয়ন করে পায়,

9x + 6y = 18

4x – 6y = 34
________________
13x = 52

x= 4

(i) নং সমীকরণে x = 4 বসিয়ে পায়

3x + 2y = 6

বা, 3 $\times$ 4 + 2y = 6

বা, 12 + 2y = 6

বা, 2y = 6 – 12

বা, 2y = -6

বা, y = -3

নির্ণেয় সমাধান x = 4 এবং y = -3

(ii) 2x + 3y = 32 , 11y – 9x = 3

2x + 3y = 32 ……………(i)

3y + 2x = 32 ……………(i)

11y – 9x = 3 ……………(ii)

(i) নং সমীকরণকে 9 দিয়ে ও (ii) নং সমীকরণকে 2 দিয়ে গুন করে x চলকে অপনয়ন করে পায়,

27y + 18x = 288

22y – 18x = 6
_____________________
49y = 294

y = 6

(ii) নং সমীকরণে y = 6 বসিয়ে পাই,

11y – 9x = 3

বা, 11 $\times$ 6 – 9x = 3

বা, 66 – 9x = 3

বা, -9x = 3 – 66

বা, -9x = -63

বা, -x = -7

বা, x = 7

নির্ণেয় সমাধান x = 7 এবং y = 6

(iii) x + y = 48; x + y = $\frac{5}{2}$(y + 4)

x + y = 48 ………….(i)

x + y = $\frac{5}{2}$(y + 4)

বা, 2x + 8 = 5y + 20

বা, 2x – 5y = 20 – 8

2x – 5y = 12………….(ii)

(i) নং সমীকরণকে 5 দিয়ে ও (ii) নং সমীকরণকে 1 গুন করে y চলকে অপনয়ন করি,

5x + 5y = 240
2x – 5y = 12
___________________________
7x = 252
বা, x = 36

(i) নং সমীকরণে x = 36 বসিয়ে পাই,

x + y = 48

বা, 36 + y = 48

বা, y = 12

নির্ণেয় সমাধান x = 36 এবং y = 12

(iv) $\frac{x}{2} + \frac{y}{3}$ = 4 ; $\frac{5x}{4}$ – 3y = -3

$\frac{x}{2} + \frac{y}{3}$ = 4 ……………(i)

বা, $\frac{3x + 2y}{6} = 8$

বা, 3x + 2y = 48 ………..(iii)

$\frac{5x}{4}$ – 3y = -3……………..(ii)

বা, $\frac{5x – 12y}{4} = -3$

বা, 5x – 12y = -12………….(iv)

(iii) সমীকরণকে 6 দিয়ে (iv) সমীকরণে 1 দিয়ে গুন করে y চলকে অপনয়ন করি,

18x + 12y = 288
5x – 12y = -12
__________________
23x = 276

x = 12

(iii) নং সমীকরণে x = 12 বসিয়ে পাই,

3x + 2y = 48

বা, 3 $\times$ 12 + 2y = 48

বা, 36 + 2y = 48

বা, 2y = 12

বা, y = 6

নির্ণেয় সমাধান x = 12 এবং y = 6

(v) 3x – $\frac{2}{y}$ = 5 ; x + $\frac{4}{y}$ = 4

সমাধান: 3x – $\frac{2}{y}$ = 5………….(i) ×2

x + $\frac{4}{y}$ = 4 ……………..(ii) × 1

6x – $\frac{4}{y}$ = 10…………..(iii)

x + $\frac{4}{y}$ = 4 ……………(iv)
______________________________________

7x = 14

বা, x = 2

(i) নং সমীকরণে x = 2 বসিয়ে পায়

3 × 2 – $\frac{2}{y}$ = 5

$\frac{2}{y}$ = 6-5 = 1

y = 2

নির্ণেয় সমাধান x = 2, y = 2

(vi) $\frac{x}{2}+\frac{y}{3}$ = 1 ; $\frac{x}{3}+ \frac{y}{2}$ = 1

সমাধান: $\frac{x}{2}+{y}{3}$ = 1

$\frac{3x + 2y}{6}$ = 1

বা, 3x + 2y = 6……….(i) × 2

$\frac{x}{3}+ \frac{y}{2}$ = 1

$\frac{2x + 3y}{6}$ = 1

বা, 2x + 3y = 6 ………..(ii) × 3

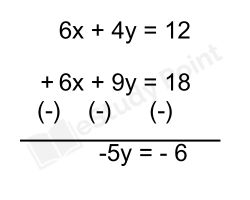
y = $\frac{6}{5}$

(i) নং সমীকরণে x = $\frac{6}{5}$ বসিয়ে পায়

3 × $\frac{6}{5}$ + 2y = 6

2y = 6 – $\frac{18}{5} = \frac{12}{5}$

y = $\frac{6}{5}$

নির্ণেয় সমাধান x = $\frac{6}{5}$ , y = $\frac{6}{5}$

(vii) $\frac{x+y}{2} + \frac{3x-5y}{4}$ = 2; $\frac{x}{14} + \frac{y}{18}$ = 1

সমাধান: $\frac{x+y}{2} + \frac{3x-5y}{4}$ = 2

বা, $\frac{4x + 4y + 6x – 10y}{8}$ = 2

বা, $\frac{10x – 6y}{8}$ = 2

বা, 10x – 6y = 16 ……….(i) ×9

$\frac{x}{14} + \frac{y}{18}$ = 1

বা, $\frac{9x + 7y}{126}$ = 1

বা, 9x + 7y = 126 ……….(ii) ×10

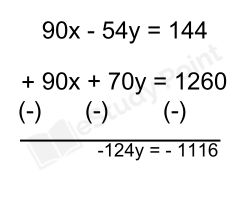
y = $\frac{-1116}{-124}$ = 9

y = 9

(i) নং সমীকরণে y=9 বসিয়ে পায়

10x – 6y = 16

বা, 10x – 6 × 9 = 16

বা, 10x – 54 = 16

বা, 10x = 16 + 54

বা, 10x = 70

বা, x = 7

নির্ণেয় সমাধান x = 7 এবং y = 9

(viii) $\frac{xy}{x+y} = \frac{1}{5} ; \frac{xy}{x-y} = \frac{1}{9}$

সমাধান : $\frac{xy}{x+y} = \frac{1}{5}$

বা, $\frac{1}{x} + \frac{1}{y}= 5$………(i)

$\frac{xy}{x-y} = \frac{1}{9}$

বা, $\frac{1}{y} – \frac{1}{x}=9$…………(ii)

বা, $(\frac{1}{y}- \frac{1}{x}) + (\frac{1}{x}+{1}{y})$ = 9+5

বা, $\frac{1}{y}- \frac{1}{x} + \frac{1}{x}+{1}{y}$ = 14

বা, $\frac{2}{y} = 14$

বা, $\frac{1}{y} = 7$

(i) নং সমীকরণে বসিয়ে$\frac{1}{y} = 7$ পায়

বা, $\frac{1}{x} + \frac{1}{y}= 5$

বা, $\frac{1}{x}+\frac{1}{\frac{1}{7}} = 5$

বা, $\frac{1}{x}+ 7 = 5$

বা, $\frac{1}{x} = 5-7$

বা, $\frac{1}{x} = -2$

বা, $x = -\frac{1}{2}$

নির্ণেয় সমাধান $x = -\frac{1}{2} ; y = \frac{1}{7}$

(ix) $\frac{1}{x-1} + \frac{1}{y-2} = 3 ; \frac{2}{x-1} + \frac{3}{y-2} = 5$

সমাধান:

মনে করি, $\frac{1}{x-1} = a$ এবং $\frac{1}{y-2} = b$

$\frac{1}{x-1} + \frac{1}{y-2} = 3$

a + b = 3……….(i) × 2

$\frac{2}{x-1} + \frac{3}{y-2} = 5$

2a + 3b = 5……….(ii) ×1

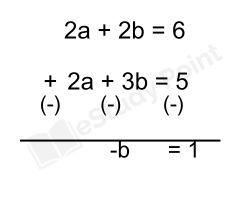
b = -1

(i) নং সমীকরণে b = -1 বসিয়ে পাই

a + b = 3

বা, a + (-1) = 3

বা, a = 3+1

বা, a = 4

$\frac{1}{x-1} = a$

বা, $\frac{1}{x-1} = 4$

বা, 4x – 4 = 1

বা, 4x = 1 + 4

বা, 4x = 5

বা, x = $\frac{5}{4}$

বা, $\frac{1}{y-2} = b$

বা, $\frac{1}{y-2} = -1$

বা, -y + 2 = 1

বা, -y = 1 -2

বা, -y = -1

বা, y = 1

(x) $\frac{14}{x+y} + \frac{3}{x-y} = 5 ; \frac{21}{x+y} – \frac{1}{x-y} = 2$

ধরি, $\frac{1}{x+y} = a$ এবং $\frac{1}{x-y} = b$

$\frac{14}{x+y} + \frac{3}{x-y} = 5 $

14a + 3b = 5…………..(i) ×1

আবার, $\frac{21}{x+y} – \frac{1}{x-y} = 2$

21a – b = 2……………..(ii) ×3

14a + 3b =5

63a – 3b = 6
________________
77a = 11

বা, a = $\frac{11}{77}$

বা, a = $\frac{1}{7}$

(i) নং সমীকরণে a = $\frac{1}{7}$ বসিয়ে পাই

14a + 3b = 5

14 × ($\frac{1}{7}$) + 3b =5

বা, 2 + 3b = 5

বা, 3b = 5 – 2

বা, 3b = 3

বা, b = 1

$\frac{1}{x+y} = a$

বা, $\frac{1}{x+y} = \frac{1}{7}$

বা, x+y = 7 …………..(iii)

$\frac{1}{x-y} = b$

বা, $\frac{1}{x-y} = 1$

বা, x-y = 1 …………(iv)

(iii) ও (iv) নং সমীকরণকে যোগ করে পাই

(x+y) + (x-y) = 7 + 1

বা, x+y+x-y = 8

বা, 2x = 8

বা, x = 4

(iii) নং সমীকরণে x=4 বসিয়ে পাই

x+y = 7

বা, 4 + y = 7

বা, y = 7-4

বা, y = 3

নির্ণেয় সমাধান x=4 , y=3

(xi) $\frac{x+y}{5} – \frac{x-y}{4} = \frac{7}{20} ; \frac{x+y}{3} – \frac{x-y}{2} + \frac{5}{6} = 0$

$\frac{x+y}{5} – \frac{x-y}{4} = \frac{7}{20}$

বা, $\frac{(4x+4y) – (5x-5y)}{20} = \frac{7}{20}$

বা, $\frac{4x+4y – 5x+5y}{20} = \frac{7}{20}$

বা, -x + 9y = 7 ………….(i)

$\frac{x+y}{3} – \frac{x-y}{2} + \frac{5}{6} = 0$

বা, $\frac{(2x+2y)-(3x-3y)+5}{6} = 0$

বা, $\frac{2x+2y-3x+3y)+5}{6} = 0$

-x + 5y = -5………….(ii)

(i) – (ii) করে পাই

(-x+9y) – (-x+5y) = 7 – (-5)

বা, -x + 9y + x – 5y = 7 + 5

বা, 4y = 12

বা, y = 3

(i) নং সমীকরণে y = 3 বসিয়ে পাই

-x + 9y = 7

বা, -x + 27 = 7

বা, -x = 7 – 27

বা, -x = -20

বা, x = 20

নির্ণেয় সমাধান x = 20 , y = 3

(xii) x+y = a+b ; ax-by = a² – b²

সমাধান: x+y = a+b ………….(i) ×b

বা, bx + by = ab + b²………….(iii)

ax-by = a² – b²……………..(ii)

(iii) ও (ii) নং সমীকরণকে যোগ করে পাই

(bx + by) + (ax – by) = (ab + b²) + (a² – b²)

বা, bx + by + ax – by = ab + b² + a² – b²

বা, bx + ax = ab + a²

বা, x(b+a) = a(b+a)

বা, x = a

(i) নং সমীকরণে x=a বসিয়ে পাই

x+y = a+b

বা, a + y = a + b

বা, y = a + b – a

বা, y = b

নির্ণেয় সমাধান x=a, y= b

(xiii) $\frac{x+a}{a} = {y+b}{b}$, ax – by = a² – b²

$\frac{x+a}{a} = {y+b}{b}$………….(i)

বা, b(x+a) = a(y+b)

বা, bx +ab = ay +ab

বা, bx –ay = 0 ……….(ii)

ax – by = a² – b² …………..(iii)

(ii) নং সমীকরণকে b দিয়ে ও (iii) নং সমীকরণকে a দিয়ে গুন করে y কে অপনয়ন করে পাই

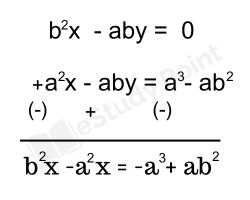
বা, b²x – a²x = ab² – a³

বা, x (b² – a²) = a (b² – a²)

বা, x = a

(ii) নং সমীকরণে x = a বসিয়ে পাই

bx –ay = 0

বা, b (a) – ay = 0

বা, ab = ay

বা, y = b

∴ নির্ণেয় সমাধান x = a এবং y = b

বিঃদ্রঃ Class 9 Math Kose Dekhi 5.3 অধ্যায়ের মধ্যে যদি তোমরা কোনো অঙ্কের সমাধান দেখতে না পাও অথবা কোথাও যদি ভুল খুঁজে পাও তাহলে অবশ্যই আমাদের জানাবে

রৈখিক সহ সমীকরণ Kose Dekhi 5.1

রৈখিক সহ সমীকরণ Kose Dekhi 5.4

নবম শ্রেনীর গণিতের সকল অধ্যায়ের সমাধান