প্রিয় ছাত্র ছাত্রী তোমাদের প্রয়োজনমত সব প্রশ্নের উত্তর দেওয়ার জন্য আমরা এই estudypoint.com ওয়েবসাইট বানিয়েছি। আজকের এই পোস্টে আমরা মধ্য শিক্ষা পর্ষদের নবম শ্রেণীর ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল : কষে দেখি 15.2 ক্লাস 9 এই চ্যাপ্টারের গণিতের সম্পূর্ণ উত্তর দিয়েছি।
যদি তোমাদের আরো ও গণিতের সমাধানের প্রয়োজন হয় তাহলে আমাদের এই ওয়েবসাইটের কমেন্ট বক্সে লিখে জানাবে। আমরা চেষ্টা করবো যত তাড়াতাড়ি তোমাদের প্রশ্নের উত্তর দিতে পারি।
1. নীচের ছবিগুলির ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ।
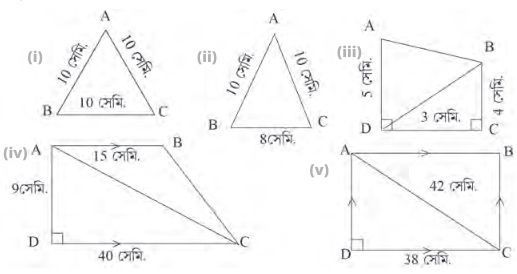
(i) ABC ত্রিভুজটি একটি সমবাহু ত্রিভুজ যার AB=BC=CA=10 সেমি.
ত্রিভুজটির ক্ষেত্রফল = $\frac{\sqrt{3}}{4} \times$ (বাহু)2
= $\frac{\sqrt{3}}{4} \times (10)^2 = \frac{\sqrt{3}}{4} \times 100 = 25\sqrt{3}$
(ii) ABC ত্রিভুজের AB = AC = 10 সেমি. এবং BC = 8 সেমি.
= 12 $\times 8 \times \sqrt{(10)^2 – \frac{8^2}{4}}$
= 4 $\times \sqrt{100 – \frac{64}{4}}$
= 4 x $\sqrt {100 – 16} = 4 \times \sqrt{84} = 8 \sqrt{21}$
= ত্রিভুজটির ক্ষেত্রফল 8$\sqrt{21}$ বর্গসেমি.
(iii) ABCD চতুর্ভুজের AD || BC
∴ ABCD একটি ট্রাপিজিয়াম ।
আবার , CD ⊥ AD এবং CD ⊥ BC
∴ CD , ABCD ট্রাপিজিয়ামের উচ্চতা ।
ABCD ট্রাপিজিয়ামের ক্ষেত্রফল
= $\frac{1}{2}$ ✕ (সমান্তরাল বাহুদ্বয়ের যোগফল ) ✕ উচ্চতা
= $\frac{1}{2}$ ✕ (AD + BC) ✕ CD
= { $\frac{1}{2}$ ✕(5+4) ✕ 3 } বর্গ সেমি.
= $\frac{27}{2}$ বর্গ সেমি.
= 13.5 বর্গ সেমি.
(iv) ABCD ট্রাপিজিয়ামের ক্ষেত্রফল
= $\frac{1}{2} \times (40 + 15) \times 9$ বর্গ সেমি
= $\frac{1}{2} \times 55 \times$ বর্গ সেমি
= 247.5 বর্গ সেমি
(v) ABCD চতুর্ভুজের AB || DC এবং AD || BC , অর্থাৎ বিপরীত বাহুগুলি পরস্পর সমান্তরাল এবং ∠ADC = 90
∴ ABCD একটি আয়তক্ষেত্র
এখন , ADC সমকোণী ত্রিভুজ থেকে পাই ,
AD2 +CD2 = AC2
বা, AD2 + (38)2 = (42)2
বা, AD2 = (42)2 –(38)2
বা, AD2 = (42+38) (42-38)
বা, AD2 = 80 ✕ 4
বা, AD2 = 320
বা, AD = 8√5
2. কোনো সমবাহু ত্রিভুজের পরিসীমা 48 সেমি. হলে তার ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান :
সমবাহু ত্রিভুজের পরিসীমা = 48 সেমি
সমবাহু ত্রিভুজের একটি বাহুর দৈর্ঘ্য = $\frac{48}{3}$ = 16 সেমি
সমবাহু ত্রিভুজটির ক্ষেত্রফল = $\frac{\sqrt{3}}{4} \times (16^2)$ বর্গ সেমি
= $\frac{\sqrt{3} \times 16 \times 16}{4}$ বর্গসেমি
= 64√3
3. ABC সমবাহু ত্রিভুজের উচ্চতা 5√3 সেমি. হলে , ত্রিভুজটির পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান:
সমবাহু ত্রিভুজটির উচ্চতা 5√3 সেমি
শর্তানুযায়ী, $\frac{\sqrt{3}}{2} \times$ বাহু = 5√3
বা, বাহু = $\frac{5\sqrt{3} \times 2}{\sqrt{3}}$
বা, বাহু = 10
ত্রিভুজটির বাহুর দৈর্ঘ্য 10 সেমি
ত্রিভুজটির পরিসীমা = (3 x 10) = 30 সেমি
এবং উহার ক্ষেত্রফল = $\frac{\sqrt{3}}{4} \times (10^2)$ বর্গসেমি
= 25√3
4. ABC সমদ্বিবাহু ত্রিভুজের সমান বাহুদুটির প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং ভূমির দৈর্ঘ্য 4 সেমি হলে , ABC এর ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান:
আমরা জানি, সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল
= 1/2 x ভূমির দৈর্ঘ্য x √(সমান বাহুর একটির দৈর্ঘ্য)2 – √(ভূমির দৈর্ঘ্যর অর্ধেক)2
= $\frac{1}{2} \times 4 \times \sqrt{(10)^2 – (2)^2}$
= 2√96
= 8√6
ABC ত্রিভুজের ক্ষেত্রফল 8√6 বর্গসেমি
5. যদি কোনো সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য 12 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য 10 সেমি. হয় , তবে ওই সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান:
আমরা জানি, সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল
= 1/2 x ভূমির দৈর্ঘ্য x √(সমান বাহুর একটির দৈর্ঘ্য)2 – √(ভূমির দৈর্ঘ্যর অর্ধেক)2
= $\frac{1}{2} \times 4 \times \sqrt{(10)^2 – 2^2}$
= 2√96 = 8√6
6. কোনো সমদ্বিবাহু ত্রিভুজের পরিসীমা 544 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য ভূমির দৈর্ঘ্যের 5/6 অংশ ; ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান:
মনে করি, সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য a সেমি
সমান বাহুর প্রত্যেকটির দৈর্ঘ্য = $\frac{5a}{6}$
আবার সমদ্বিবাহু ত্রিভুজটির পরিসীমা 544 সেমি
শর্তানুযায়ী,
a + (2 x 5a/6) = 544
বা, a + 5a/3 = 544
বা, $\frac{3a + 5a}{3}$ = 544
বা, 8a = 1632
বা, a = 204
এবং সমান বহু দুটির প্রত্যেকটির দৈর্ঘ্য = $\frac{5 \times 204}{6}$ = 160 সেমি
ত্রিভুজটির ক্ষেত্রফল = $\frac{1}{2} \times 204 \times \sqrt{(170)^2 – (\frac{204}{2})^2}$ বর্গসেমি
= 102 x $\sqrt{(170)^2 – (102)^2}$
= 102 x $\sqrt{272 \times 68}$
= 102 x $\sqrt{16 \times 17 \times 4 \times 17}$
= 102 x 4 x 17 x 2
= 12872 বর্গসেমি
7. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজের দৈর্ঘ্য 12√2 সেমি. হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান:
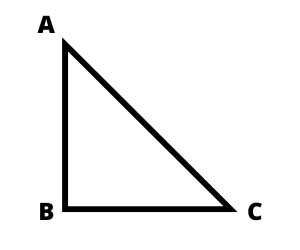
মনে করি, ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার AB = BC এবং অতিভুজ AC = 12√2
শর্তানুযায়ী, 2AB2 = AC2
বা, 2AB2 = (12√2)2
বা, 2AB2 = 144 x 2
বা, AB2 = 144
বা, AB = 12
AB = BC = 12 সেমি
ত্রিভুজটির ক্ষেত্রফল = ($\frac{1}{2}$ X 12 X 12) = 72 বর্গসেমি
8. পৃথা একটি সামান্তরিক এঁকেছে যার কর্ণদ্বয়ের দৈর্ঘ্য যথাক্রমে 6 সেমি. ও 8 সেমি. এবং কর্ণদ্বয়ের মধ্যবর্তী কোণগুলির প্রত্যেকটি 90°; সামান্তরিকের বাহুগুলির দৈর্ঘ্য লিখি এবং সামান্তরিকটির বৈশিষ্ট্য লিখি ।
সমাধান:
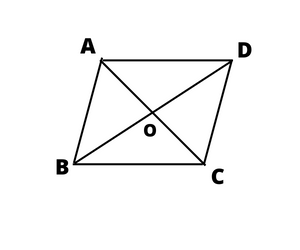
যেহেতু সামান্তরিক কর্ন্দ্বয়ের মধ্যবর্তী কোনগুলি প্রত্যেকটি 90° সুতরাং সামান্তরিক আয়াত্ক্ষেত্রে বা রম্বস|
কিন্তু সামান্তরিক কর্ন্দ্বয়ের দৈর্ঘ্য ভিন্ন
সুতরাং সামান্তরিক আয়াত্খেত্রে নয় ইহা একটি রম্বস
স্পষ্ট আমরা দেখতে পাচ্ছি, কর্ন AC = 6 সেমি এবং BD = 8 সেমি
আমরা জানি , রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদিখন্দিত করে
AO = OC = 3 সেমি
এবং BO = OD = 4 সেমি
এখন OCD সমকোণী ত্রিভুজ হতে পাই
CD2 = OC2 + OD2
CD2 = 32 + 42
CD2 = 9 + 16 = 25
CD = 5
সুতরাং সামান্তরিকের বাহুগুলি প্রত্যেকের দৈর্ঘ্য 5 সেমি এবং সামান্তরিকের একটি রম্বস
9. আমাদের পাড়ার ত্রিভুজাকৃতি একটি পার্কের বাহুগুলির দৈর্ঘ্যের অনুপাত 2:3:4 ; পার্কটির পরিসীমা 216 মিটার ।
(i) হিসাব করে পার্কটির ক্ষেত্রফল লিখি ।
(ii) পার্কটির বৃহত্তম বাহুর বিপরীত বিন্দু থেকে ওই বাহুতে সোজাসুজি যেতে কত পথ হাঁটতে হবে হিসাব করে লিখি ।
সমাধান:
(i) ত্রিভূজাকৃতি পার্কটির বাহুগুলির দৈর্ঘ্য অনুপাত = 2 : 3 : 4
মনেকরি, পার্কটির বাহুগুলির দৈর্ঘ্য 2x মি. , 3x মি., 4x মি.
শর্তানুযায়ী,
2x + 3x + 4x = 216
বা, 9x = 216
বা, x = $\frac{216}{9}$
বা, x = 24
পার্কটির বাহুগুলির দৈর্ঘ্য 48 মি. , 72 মি. , 96 মিটার পার্কটির অর্ধপরিসীমা S =
ত্রিভুজকৃতি পার্কটির ক্ষেত্রফল
= $\sqrt{108(108 – 48) (108 – 72) (108 – 96)}$ বর্গমিটার
= $\sqrt{108 \times 60 \times 36 \times 12} = 432\sqrt{15}$ বর্গমিটার
(ii) পার্কটির বৃহত্তম বাহুর দৈর্ঘ্য 96
আবার বৃহত্তম বাহুর বিপরীত কৌনিক বিন্দু থেকে ওই বাহুতে সোজাসুজি যেতে হলে কৌনিক বিন্দু থেকে ওই বাহুতে লম্ব হবে
শর্তানুযায়ী,
$\frac{1}{2} \times 96 \times x = 432\sqrt{15}$
বা, x = $\frac{2 \times 432\sqrt{15}}{96}$
বা, x = $\frac{432\sqrt{15}}{48} = 9\sqrt{15}$
অর্থাৎ ,পার্কের বৃহত্তম বাহু থেকে বিপরীত কৌণিক বিন্দু পর্যন্ত হাঁটতে হলে 9√15 মিটার দূরত্ব অতিক্রম করতে হবে ।
10.পহলমপুর গ্রামের ত্রিভুজাকৃতি মাঠের তিনদিকের দৈর্ঘ্য যথাক্রমে 26 মিটার , 28 মিটার ও 30 মিটার ।
(i) প্রতি বর্গমিটার 5 টাকা হিসাবে ত্রিভুজাকৃতি মাঠে ঘাস লাগাতে মোট কত টাকা খরচ হবে হিসাব করে লিখি ।
(ii) ওই ত্রিভুজাকৃতি মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে বাকি চারধার বেড়া দিয়ে ঘিরতে প্রতি মিটার 18 টাকা হিসাবে মোট কত টাকা খরচ হবে হিসাব করে লিখি ।
সমাধান:
ত্রিভূজাকৃতি মাঠটির তিনটি বাহুর দৈর্ঘ্য 26মিটার, 28 মিটার, ও 30 মিটার
ত্রিভুজাকৃতি মাঠের পরিসীমা = (26+28+30) মিটার = 84 মিটার
∴ মাঠটির অর্ধ পরিসীমা (s) = $\frac{84}{2}$ মিটার = 42 মিটার।
মাঠটির ক্ষেত্রফল = $\sqrt{42 \times (42 – 26)(42-28)(42-30)}$ বর্গমিটার
= $\sqrt{42 \times 16\times 14 \times 12}$ বর্গমিটার
= $\sqrt{7\times 3\times 2\times 4\times 4\times 2\times 7 \times 4 \times 3}$ বর্গমিটার
= 7 x 2 x 4 x 2 x 3 = 336 বর্গমিটার
∴ প্রতি বর্গমিটারে 5 টাকা হিসাবে ত্রিভুজাকৃতি মাঠে ঘাস লাগাতে মোট খরচ হবে (336 x 5) = 1680 টাকা
(ii) ত্রিভুজাকার মাঠটির পরিসীমা = 42 x 2 = 84 মিটার
∴ 5 মিটার জায়গা ছেড়ে বেড়া দিতে হলে মোট 79 মিটার বেড়া দিতে হবে
∴ মাঠটি বেড়া দিতে খরচ পড়বে = (79 x 18) = 1422 টাকা
11. শাকিল একটি সমবাহু ত্রিভুজ PQR এঁকেছে । আমি ওই সমবাহু ত্রিভুজের অন্তস্থঃ কোনো বিন্দু থেকে ত্রিভুজের বাহ গুলির ওপর তিনটি লম্ব অঙ্কন করেছি যাদের দৈর্ঘ্য যথাক্রমে 10 সেমি. ,12 সেমি. এবং 8 সেমি. । হিসাব করে PQR ত্রিভুজের ক্ষেত্রফল লিখি ।
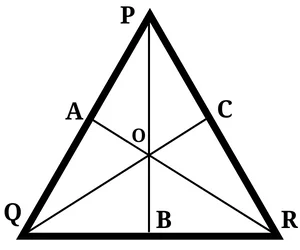
ধরা যাক, PQR একটি সমবাহু ত্রিভুজ যার PQ = QR = RP;
ধরি, PQ = QR = RP = a সেমি
ত্রিভুজটির অন্তঃস্থ বিন্দু O থেকে তিনটি বাহুর উপর লম্ব OA, OB এবং OC
OA = 10সেমি , OB = 12সেমি , OC = 8 সেমি
$\triangle PQR = \triangle OPQ + \triangle OQR + \triangle ORP$
$\frac{\sqrt{3}}{4} a^2 = \frac{1}{2} \times a \times 10+ \frac{1}{2} \times a \times 12 + \frac{1}{2} \times a \times 8$
$\frac{\sqrt{3}}{4} a^2$ = 5a + 6a + 4a
$\frac{\sqrt{3}}{4} a^2$ = 15a
a = $\frac{15 \times 4}{\sqrt{3}} = 20\sqrt{3}$
$\triangle PQR$ এর ক্ষেত্রফল = $(\frac{\sqrt{3}}{4} \times 20\sqrt{3} \times 20\sqrt{3})$ বর্গসেমি
$ = 300\sqrt{3}$ বর্গসেমি
12. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 45° হলে , ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান:
ধরা যাক ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB = BC = 20 সেমি এবং $\angle$ BAC = 45°
এখন B বিন্দু থেকে AC বাহুর উপর লম্ব অঙ্কন করা হল
অর্থাৎ $\angle BDA$ = 90°
Sin $\angle BAD = \frac{BD}{AB}$
Sin 45° = $\frac{BD}{20}$
BD = 20 $\times \frac{1}{\sqrt{2}} = 10\sqrt{2}$
$\angle ABC$ এর ক্ষেত্রফল = $\frac{1}{2} \times BD \times AC$
= $\frac{1}{2} \times 10\sqrt{2} \times 20 = 100\sqrt{2}$ বর্গসেমি
13. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 30° হলে , ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান :
ধরি ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB = BC = 20 সেমি এবং $\angle$ BAC = 30° এখন B বিন্দু হতে AC বাহুর উপর BD লম্ব অঙ্কন করা হল
অর্থাৎ $\angle$ BDA = 90°
$\triangle$ ABD হতে পাই
Sin $\angle$ BAD =$\frac{BD}{AB}$
বা, Sin 30° = $\frac{BD}{20}$
বা, BD = $\frac{1}{2} \times $ 20
বা, BD = 10
∴ $\triangle$ ABC এর ক্ষেত্রফল = $\frac{1}{2} \times BD \times AC = \frac{1}{2} \times 10 \times$ 20
= 100 বর্গসেমি
∴ ত্রিভুজটির ক্ষেত্রফল 100 বর্গসেমি
14. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা (√2+1) সেমি. হলে, ত্রিভুজটির অতিভুজের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি ।
সমাধান: মনে করি সমদ্বিবাহু ত্রিভুজটির সমান বহু দুটির প্রত্যেকতির দৈর্ঘ্য a সেমি
আবার যেহেতু সমদ্বিবাহু ত্রিভুজটির সমকোণী
সুতরাং a2 + a2 = (অতিভুজ)2
2a2 = (অতিভুজ)2
অতিভুজ = $\sqrt{2a}$
শর্তানুযায়ী,
a + a + $\sqrt{2a} = \sqrt{2}$ + 1
বা, a (1+1+$\sqrt{2}$) = $\sqrt{2}$ + 1
a = $\frac{\sqrt{2}+1}{2 + \sqrt{2}} = \frac{(\sqrt{2}+1)(2-\sqrt{2})}{4-2} = \frac{2\sqrt{2}+2-2-\sqrt{2}}{2}$
= $\frac{2\sqrt{2}-\sqrt{2}}{2} = \frac{\sqrt{2}(2-1)}{2} = \frac{\sqrt{2}}{2}$
অতিভুজের দৈঘ্য = $\sqrt{2} \times \frac{\sqrt{2}}{2}= \frac{2}{2}$ = 1 সেমি
ত্রিভুজটির ক্ষেত্রফল = $\frac{1}{2} \times \frac{\sqrt{2}}{2} \times \frac{\sqrt{2}}{2} = \frac{1}{4}$ = 0.25 বর্গসেমি
15. মারিয়া ঘণ্টায় 18 কিমি. বেগে সাইকেল চালিয়ে 10 মিনিটে একটি সমবাহু ত্রিভুজাকার মাঠের পরিসীমা বরাবর ঘুরে এল । ত্রিভুজটির একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত সোজা যেতে মারিয়ার কত সময় লাগবে হিসাব করে লিখি । (√3 = 1.732 )
সমাধান:
