প্রিয় ছাত্র ছাত্রী তোমাদের প্রয়োজনমত সব প্রশ্নের উত্তর দেওয়ার জন্য আমরা এই estudypoint.com ওয়েবসাইট বানিয়েছি। আজকের এই পোস্টে আমরা মধ্য শিক্ষা পর্ষদের নবম শ্রেণীর বৃত্তের ক্ষেত্রফল : কষে দেখি 18 class 9 এই চ্যাপ্টারের গণিতের সম্পূর্ণ উত্তর দিয়েছি।
যদি তোমাদের আরো ও গণিতের সমাধানের প্রয়োজন হয় তাহলে আমাদের এই ওয়েবসাইটের কমেন্ট বক্সে লিখে জানাবে। আমরা চেষ্টা করবো যত তাড়াতাড়ি তোমাদের প্রশ্নের উত্তর দিতে পারি।
Wbbse Class 9 Math All Chapter Solution
Koshe Dekhi 18 Class 9
1. আমিনাবিবি আজ 2.1 মিটার লম্বা একটি দড়ি দিয়ে তার গােরুটিকে ফাঁকা মাঠে খুঁটির সঙ্গে বাঁধলেন। হিসাব করে দেখি গােরুটি সবথেকে বেশি কতটা জমির ঘাস খেতে পারবে।
সমাধান:
2.1 মিটার ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফল = $\pi\times r^2$
= $\frac{22}{7} \times 2.1 \times 2.1 $
= 13.86 বর্গমিটার
2. সুহানা একটি বৃত্ত আঁকবে যার পরিধি হবে 35.2 সেমি। হিসাব করে দেখি সুহানা যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য কত নেবে এবং বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল কত হবে।
সমাধান:
মনে করি, সুহানা যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য r সেমি.
শর্তানুসারে: 2πr = 35.2
বা, 2 $\times \frac{22}{7} \times$ r = 35.2
বা, r = $\frac{35.2 \times 7}{2 \times 22}$
বা, r = 5.6
বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল = πr2 = $\frac{22}{7} \times 5.6 \times 5.6$ = 98.56 বর্গসেমি
3. রেখার দিদিমা একটি গােলাকার টেবিলের ঢাকনা তৈরি করেছেন যার ক্ষেত্রফল 5544 বর্গ সেমি.। তিনি এই টেবিলের ঢাকনার চারিদিকে রঙিন ফিতে লাগাতে চান। হিসাব করে দেখি দিদিমাকে কত দৈর্ঘ্যের রঙিন ফিতে কিনতে হবে।
মনে করি, গোলাকার টেবিলের ঢাকনার ব্যাসার্ধ r সেমি.
শর্তানুসারে, πr2 = 5544
বা, $\frac{22}{7} \times r^2$ = 5544
বা, r2 = $\frac{5544 \times 7}{22}$
বা, r2 = 36 X 7 X 7
বা, r = $\sqrt{36\times 7\times 7}$
বা, r = 6 X 7
বা, r = 42
∴ এখন 2πr = $ 2\times \frac{22}{7} \times 42$ = 264 সেমি.
4. আমাদের পাড়ার বৃত্তাকার খেলার মাঠটি বেড়া দিয়ে ঘিরতে প্রতি মিটার 21 টাকা হিসাবে 924 টাকা খরচ হয়েছে। মাঠটি ত্রিপল দিয়ে ঢেকে দেওয়ার জন্য কত বর্গমিটার ত্রিপল কিনতে হবে হিসাব করে লিখি।
লেখার মাঠটি বেড়া দিতে 21 টাকা খরচ হয় 1 মিটারে
লেখার মাঠটি বেড়া দিতে 1 টাকা খরচ হয় $\frac{1}{21}$ মিটারে
লেখার মাঠটি বেড়া দিতে 924 টাকা খরচ হয় $\frac{924}{21}$ মিটারে = 44 মিটার
বৃত্তাকার খেলার মাঠটির পরিসীমা 44 মিটার
মনে করি, খেলার মাঠটির ব্যাসার্ধ r মিটার
শর্তানুসারে, 2πr = 44
বা, 2 $\times \frac{22}{7} \times$ r = 44
বা,r = $\frac{44 \times 7}{44}$
বা, r = 7
∴ খেলার মাঠটির ক্ষেত্রফল = $\frac{22}{7} \times 7^2$ = 154 বর্গমিটার
উত্তর: মাঠটি ত্রিপল দিয়ে ঢেকে দেওয়ার জন্য 154 বর্গমিটার ত্রিপল কিনতে হবে
5. ফারুক একটি বৃত্ত আঁকবে যার ক্ষেত্রের ক্ষেত্রফল হবে 616 বর্গসেমি.। হিসাব করে দেখি ফারুক যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য কত নেবে এবং বৃত্তটির পরিধি কত পাবে।
মনে করি, ফারুক যে বৃত্ত আঁকবে তার ব্যসার্ধের দৈর্ঘ্য r সেমি
শর্তানুসারে, πr2 = 616
বা, $\frac{22}{7} \times r^2$ = 616
বা, r2 = $\frac{616 \times 7}{22}$
বা, r = 14
∴ বৃত্তটির পরিধি = 2πr = $2 \times \frac{22}{7} \times$ 14 = 88 সেমি.
উত্তর: ফারুক যে বৃত্ত আঁকবে তার ব্যসার্ধের দৈর্ঘ্য 14 সেমি এবং বৃত্তটির পরিধি 88 সেমি.
6. পলাশ ও পিয়ালী দুটি বৃত্ত এঁকেছে যাদের ব্যাসার্ধের দৈর্ঘ্য অনুপাত 4 : 5; হিসাব করে দুজনের আঁকা বৃত্তাকার ক্ষেত্র দুটির ক্ষেত্রফলের অনুপাত লিখি।
মনে করি, বৃত্তদুটির ব্যাসার্ধ 4r একক এবং 5r একক
∴ বৃত্তদুটির ক্ষেত্রফলের অনুপাত = π(4r)2 : π(5r)2
= 16πr2 : 25πr2 = 16 : 25
দুজনের আঁকা বৃত্তাকার ক্ষেত্র দুটির ক্ষেত্রফলের অনুপাত 16 : 25
7. সুমিত ও রেবা একই দৈর্ঘ্যের দুটি তামার তার এনেছে। সুমিত ওই তারটি বেঁকিয়ে আয়তাকার চিত্র তৈরি করেছে যার দৈর্ঘ্য 48 সেমি., এবং প্রস্থ 40 সেমি.। কিন্তু রেবা একই দৈর্ঘ্যের তামার তারটি বেঁকিয়ে বৃত্ত তৈরি করল। হিসাব করে দেখি সুমিতের তৈরি আয়তাকার চিত্র এবং রেবার তৈরি বৃত্তের মধ্যে কোনটি বেশি জায়গা জুড়ে থাকবে।
সুমিতের তৈরী আয়তকার চিত্রটির দৈর্ঘ্য 48 সেমি ও প্রস্থ 40 সেমি.
∴ আয়তকার চিত্রটির পরিসীমা = 2 X (48 + 40) = 176 সেমি.
রেবার তৈরী বৃত্তের পরিধি = 176 সেমি
মনে করি, বৃত্তটির ব্যসার্ধ r সেমি.
শর্তানুসারে, 2πr = 176
বা, $ 2 \times \frac{22}{7} \times r$ = 176
বা, r = $\frac{176 \times 7}{2 \times 22}$
বা, r = 4X 7
বা, r = 28
∴ রেবার তৈরী বৃত্তটির ক্ষেত্রফল = $\frac{22}{7} \times 28 \times 28$ = 2464 বর্গসেমি.
সুমিতের তৈরী আয়তাকার চিত্রটির ক্ষেত্রফল = (48 X 40) = 1920 বর্গসেমি
8. পাইওনিয়ার অ্যাথলেটিক ক্লাবের আয়তাকার মাঠের মাঝখানে একটি বৃত্তাকার জলাশয় আছে যার ব্যাসার্ধের দৈর্ঘ্য 14 মিটার। আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 60 মিটার ও 42 মিটার। জলাশয় বাদে আয়তাকার মাঠের বাকি জায়গায় ঘাস লাগাতে প্রতি বর্গমিটার 75 টাকা হিসাবে কত খরচ হবে হিসাব করে দেখি।
বৃত্তাকার জলাশয়ের ব্যাসার্ধের দৈর্ঘ্য 14 মিটার
∴ বৃত্তকার জলাশয়ের ক্ষেত্রফল = $\frac{22}{7} \times 14 \times 14$ = 616 বর্গমিটার
আয়তকার মাঠটির দৈর্ঘ্য = 60 মিটার এবং প্রস্থ = 42 মিটার
∴ আয়তাকার মাঠটির ক্ষেত্রফল = (60 X 42) = 2520 বর্গমিটার
জলাশয় বাদে মাঠটির ক্ষেত্রফল = (2520 – 616) = 1904 বর্গমিটার
∴ প্রতি বর্গমিটার 75 টাকা হিসাবে ঘাস লাগাতে খরচ হবে (1904 x 75) = 142800 টাকা
জলাশয় বাদে আয়তাকার মাঠের বাকি জায়গায় ঘাস লাগাতে প্রতি বর্গমিটার 75 টাকা হিসাবে 142800 টাকা খরচ হবে
9. ইটালগাছা ফ্রেন্ডস এসােসিয়েশন ক্লাবের বৃত্তাকার পার্কের বাইরের দিকে পরিধি বরাবর একটি 7 মিটার চওড়া রাস্তা আছে। বৃত্তাকার পার্কের পরিধি 352 মিটার হলে রাস্তাটির ক্ষেত্রফল হিসাব করে লিখি। প্রতি বর্গমিটার 20 টাকা হিসাবে রাস্তাটি বাঁধতে কত টাকা খরচ হবে হিসাব করে লিখি।
বৃত্তাকার পার্কের পরিধি 352 মিটার
ধরি, বৃত্তাকার পার্কের ব্যসার্ধ r মিটার
শর্তানুসারে,
2πr = 352
বা, $ 2 \times \frac{22}{7} \times r $ = 352
বা, r = $\frac{352 \times 7}{44}$
বা,r = 8 $\times$ 7
বা, r = 56
বৃত্তাকার পার্কটির বাইরের দিকে 7 মিটার চওড়া রাস্তা আছে
রাস্তা সহ বৃত্তকার পার্কটির ব্যাসার্ধ = (56 + 7) = 63 মিটার
∴ রাস্তা সহ বৃত্তকার পার্কটির ক্ষেত্রফল = $\frac{22}{7} \times 63 \times 63$ = 12474 বর্গমিটার
∴ রাস্তা বাদে বৃত্তাকার পার্কটির ক্ষেত্রফল = $\frac{22}{7} \times 56 \times 56$ = 9856 বর্গমিটার
রাস্তার ক্ষেত্রফল = 12474 – 9856 = 2618 বর্গমিটার
∴ প্রতিবর্গমিটার 20 টাকা হিসাবে রাস্তাটি বাঁধতে খরচ হবে = (2618 $\times$ 20) = 52360 টাকা
সুতরাং রাস্তার ক্ষেত্রফল 2618 বর্গমিটার এবং রাস্তাটি বাঁধাতে খরচ পড়বে 52360 টাকা
10. আনােয়ারাবিবি তার অর্ধবৃত্তাকার জমির চারদিকে প্রতি মিটার 18.50 টাকা হিসাবে বেড়া দিতে 2664 টাকা খরচ করেছেন। তিনি যদি তার ওই অর্ধবৃত্তাকার জমি প্রতি বর্গমিটার 32 টাকা হিসাবে চাষ করান। তাহলে মােট কত টাকা খরচ করবেন হিসাব করে লিখি।
18.50 টাকা খরচ হয় 1 মিটার জমি বেড়া দিতে
1 টাকা খরচ হয় $\frac{1}{18.50}$ মিটার জমি বেড়া দিতে
2664 টাকা খরচ হয় $\frac{2664}{18.50}$ মিটার জমি বেড়া দিতে = 144 মিটার জমি বেড়া দিতে
অর্ধবৃত্তাকার জমিটির পরিধি = 144 মিটার
মনে করি, অর্ধবৃত্তাকার জমিটির ব্যসার্ধ = r মিটার
শর্তানুসারে, πr + 2r = 144
বা, r $(\frac{22}{7} + 2)$ = 144
বা, r $(\frac{22 + 14}{7})$ = 144
বা, r = $\frac{7 \times 144 }{36}$
বা, r = 28
∴ অর্ধবৃত্তাকার জমিটির ক্ষেত্রফল = $\frac{\pi r^2}{2} = \frac{1}{2} \times \frac{22}{7} \times 28 \times 28$ = 1232 বর্গমিটার
প্রতিবর্গমিটার 32 টাকা হিসাবে জমিটি চাষ করতে খরচ হয় = (1232 X 32) = 39424 টাকা
11. আজ আমার বন্ধু রজত একই বেগে দৌড়ে স্কুলের বৃত্তাকার মাঠটি যে সময়ে একবার প্রদক্ষিণ করল একই বেগে মাঠের ব্যাস বরাবর দৌড়তে 30 সেকেণ্ড কম সময় নিল। তার গতিবেগ 9 মিটার/ সেকেণ্ড হলে স্কুলের মাঠের ক্ষেত্রফল হিসাব করে লিখি।
মনে করি, স্কুলের মাঠটির ব্যাসার্ধ r মিটার
রজতের গতিবেগ 90 মিটার/সেকেন্ড
রজত 1 সেকেন্ডে যায় 90 মিটার
রজত 30 সেকেন্ডে যায় (90 $\times$ 30) = 2700 মিটার
শর্তানুসারে, 2πr – 2r = 2700
বা, 2r $(\frac{22}{7} -1)$ = 2700
বা, 2r $(\frac{22-7}{7})$ = 2700
বা, r = $\frac{2700 \times 7}{15 \times 2}$
বা, r = 630
∴ মাঠটির ক্ষেত্রফল = $(\frac{22}{7} \times 630 \times 630)$ = 124700 বর্গমিটার
12. বকুলতলার বৃত্তাকার মাঠের বাইরের চারদিকে একটি সমপরিসরের রাস্তা আছে। রাস্তাটির বাইরের সীমারেখার দৈর্ঘ্য ভিতরের সীমারেখার দৈর্ঘ্য অপেক্ষা 132 মিটার বেশি। পথটির ক্ষেত্রফল 14190 বর্গ মি. হলে বৃত্তাকার মাঠটির ক্ষেত্রফল হিসাব করে লিখ।
মনে করি, বৃত্তাকার মাঠটির ব্যসার্ধ r মিটার
এবং রাস্তাসহ বৃত্তাকার মাঠটির ব্যাসার্ধ R মিটার
শর্তানুসারে, 2πR – 2πr = 132
বা, 2π(R-r) = 132
বা,R – r = $\frac{132\times 7}{2 \times 22}$
বা, R – r = 21 …………..(i)
আবার শর্তানুসারে, πR2 – πr2 = 14190
বা, π (R2-r2) = 14190
বা, $\frac{22}{7}$ (R – r) (R + r) = 14190
বা, (R – r) (R + r) = $\frac{14190 \times 7}{22}$
বা, (R + r) 21 = $\frac{14190 \times 7}{22}$
বা, (R + r) = $\frac{14190 \times 7}{22 \times 21}$
বা, R + r = 215……..(ii)
(i) ও (ii) নং কে যোগ করে পাই
R − r + R + r= 21 + 215
বা, 2R = 236
বা, R = $\frac{236}{2}$
বা, R = 118
(ii) নং সমীকরণে R=218 বসিয়ে পাই
R + r = 215
বা, r = 215 – 118
r = 97
বৃত্তাকার মাঠটির ব্যাসার্ধ্য 97 মিটার
∴ বৃত্তাকার মাঠটির ক্ষেত্রফল = $\frac{22}{7} \times 97 \times 97$ = 29571$\frac{1}{7}$ বর্গমিটার
13. নীচের ছবির রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল হিসাব করে লিখি।
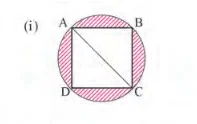
ABCD বৃত্তের পরিধি = 7 সেমি
বৃত্তের ক্ষেত্রফল = $(\frac{22}{7} \times 7 \times 7)$ = 154 বর্গসেমি
মনে করি, বর্গক্ষেটির বাহুর দৈর্ঘ্য a সেমি.
AC বর্গক্ষেত্র কর্ন
শর্তানুযায়ী, $\sqrt{2}$a = 14
বা, a = $\frac{14}{\sqrt{2}}$
∴ বর্গক্ষেত্রটির ক্ষেত্রফল = $(\frac{14}{\sqrt{2}})^2 = \frac{196}{2}$ = 98 বর্গসেমি
রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল =(154 – 98) = 56 বর্গসেমি
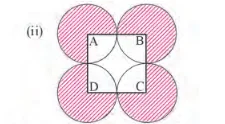
A কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 3.5 সেমি.
বৃত্তটির ক্ষেত্রফল = $(\frac{22}{7} \times 3.5 \times 3.5)$ = 38.5 বর্গসেমি
A কেন্দ্রীয় বৃত্তটির রেখাঙ্কিত অংশ ছাড়া বাকি অংশের ক্ষেত্রফল = $(\frac{90}{360}\times \frac{22}{7} \times 3.5 \times 3.5)$ বর্গসেমি
= $\frac{1}{4} \times $ 38.5 = 9.625 বর্গসেমি
∴ A কেন্দ্রীয় বৃত্তটির রেখাঙ্কিত অংশের ক্ষেত্রফল = (38.5 – 9.625) = 28.875 বর্গসেমি
∴ চিত্রটির রেখাঙ্কিত অংশের ক্ষেত্রফল = (4 $\times$ 28.875) = 115.5 বর্গসেমি
15. নীতু একটি বর্গক্ষেত্র ABCD এঁকেছে যার প্রতিটি বাহুর দৈর্ঘ্য 12 সেমি.। আমার বােন পাশের ছবির মতাে A, B, C ও D বিন্দুকে কেন্দ্র করে 6 সেমি. দৈর্ঘ্যের ব্যাসার্ধের চারটি বৃত্তচাপ এঁকেছে এবং কিছু জায়গায় নকশা এঁকেছে
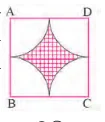
PQ বৃত্তচাপের দৈর্ঘ্য = $(\frac{90}{360} \times 2\pi \times 6) = (\frac{1}{4} \times 2 \times \frac{22}{7} \times 6)$ সেমি
নকশা আঁকা ক্ষেত্রে পরিসীমা = 4 $\times$ PQ
= 4 $\times \frac{1}{4} \times 2 \times \frac{22}{7} \times 6 = 37\frac{5}{7}$ সেমি
APQ বৃত্ত্কলার ক্ষেত্রফল = $\frac{90}{360} \times \frac{22}{7} \times 6^2 = \frac{1}{4} \times \frac{22 \times 36}{7}$ বর্গসেমি
∴ নকশা আঁকা ছাড়া বাকি অংশের ক্ষেত্রফল = $4 \times \frac{1}{4} \times \frac{22 \times 36}{7} = \frac{792}{7}$ বর্গসেমি
∴ নকশা আঁকা ক্ষেত্রের ক্ষেত্রফল = 144 – $\frac{792}{7} = \frac{1008-792}{7} = \frac{216}{7} = 30\frac{6}{7}$ বর্গসেমি
নকশা আঁকা ক্ষেত্রের পরিসীমা 37$\frac{5}{7}$ এবং ক্ষেত্রফল 30$\frac{6}{7}$ বর্গসেমি
16. একটি বৃত্তাকার মাঠের ক্ষেত্রফল 154 বর্গ সেমি.। বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রের পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি। যদি বর্গক্ষেত্রটি বৃত্তাকার মাঠের অন্তলিখিত হতাে তাহলে বর্গক্ষেত্রটির পরিসীমা ও ক্ষেত্রফল কত হতাে তা হিসাব করে লিখি।
বৃত্তাকার মাঠের ক্ষেত্রফল 154 বর্গসেমি
ধরি বৃত্তাকার মাঠের ব্যসার্ধ r সেমি
শর্তানুসারে, πr2 = 154
বা, r2 =$\frac{154 \times 7}{22}$
বা, r2 =7 X 7
বা, r = 7
∴ বৃত্তটির ব্যাসের দৈর্ঘ্য = 2 x 7 = 14 সেমি
∴ বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = 14 সেমি
∴ বর্গক্ষেত্রটির = (14)2 = 196 বর্গসেমি
যদি বর্গক্ষেত্রটি বৃত্তকার মাঠের অন্তর্লিখিত হত তাহলে বর্গক্ষেত্র কর্ণের দৈঘ্য = 14 সেমি
$\sqrt{2} \times$ বাহুর দৈর্ঘ্য = 14
বাহুর দৈর্ঘ্য = $\frac{14}{\sqrt{2}} = 7\sqrt{2}$
বর্গক্ষেত্রের ক্ষেত্রফল = (7√2)2 = 98 বর্গসেমি
18. লীনা মেলা থেকে একটি বালা কিনে হাতে পরেছে। বালাটিতে 269.5 বর্গ সেমি. ধাতু আছে। বালাটির বহির্ব্যাসের দৈর্ঘ্য 28 সেমি. হলে অন্তর্ব্যাসের দৈর্ঘ্য কত হিসাব করে লিখি।
মনে করি, বালাটির অন্তব্যাসার্ধ্য দৈর্ঘ্য r সেমি
কলাটির বহির্ব্যাসার্ধ্য দৈর্ঘ্য = $\frac{28}{2}$ = 14 সেমি
শর্তানুযায়ী , π (14)2 – πr2 = 269.5
বা, πr2 = $\frac{22}{7} \times 14 \times 14$ – 269.5
বা, $\frac{22}{7}$ r2 = 616 – 269.5
বা, r2 = $\frac{346.5 \times 7}{22}$
বা, r2 = 110.25
বা, r = 10.5
∴ অন্তব্যসার্ধ্য = (10.5 $\times$ 2) = 21 সেমি
19. প্রতুল পাশের ছবির মতাে একটি সমবাহু ত্রিভুজ ABC এঁকেছে যার প্রতিটি বাহুর দৈর্ঘ্য 10 সেমি.। সুমিতা A, B ও C বিন্দুকে কেন্দ্র করে 5 সেমি. দৈর্ঘ্যের ব্যাসার্ধের তিনটি বৃত্তচাপ এঁকেছে এবং মাঝের কিছু জায়গা রঙিন করেছে। হিসাব করে রঙিন জায়গার ক্ষেত্রফল লিখি। [√3 = 1.732 (প্রায়)]।
ABC একটি সমবাহু ত্রিভুজ
∴ ∠ABC = ∠BCA = ∠CAB = 60
APQ বৃত্ত্কলার ক্ষেত্রফল = $\frac{60}{360} \times \frac{22}{7} \times 5^2$
= $\frac{1}{6} \times \frac{22}{7} \times 25 = \frac{275}{21}$ বর্গসেমি
রঙিন অংশ বাদে ABC এর ক্ষেত্রফল = $3 \times \frac{275}{7} = \frac{275}{7}$ বর্গসেমি
ABC এর ক্ষেত্রফল = $\frac{\sqrt{3}}{4} \times 10 \times 10 = 25 \times 1.732$ = 43.3 বর্গসেমি
∴ রঙিন অংশের ক্ষেত্রফল = $(43.3 – \frac{275}{7})$ = (43.3 – 39.28) = 4.02 বর্গসেমি
20. রাবেয়া একটি বড়াে কাগজে 21 সেমি. বাহুবিশিষ্ট সমবাহু ত্রিভুজ আঁকল। ওই সমবাহু ত্রিভুজের একটি অন্তর্বৃত্ত অঙ্কন করে বৃত্তাকার জায়গাটি রঙিন করল। আমি রঙিন জায়গার ক্ষেত্রফল হিসাব করে লিখি।
সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ a = 21 সেমি
উচ্চতা = $\frac{\sqrt{3}}{2} \times 21$ সেমি
∴ ত্রিভুজের অন্তর্বৃত্তের ক্ষেত্রে বৃত্তের ব্যাসার্ধ্য হবে = $\frac{উচ্চতা}{3} = \frac{\sqrt{3} \times 21}{2 \times 3}= \frac{7\sqrt{3}}{2}$ সেমি
∴ অন্তর্বৃত্তের ক্ষেত্রফল = $\frac{22}{7} \times \frac{7\sqrt{3}}{2} \times \frac{7\sqrt{3}}{2}= \frac{11 \times 21}{2}$ = 115.5 বর্গসেমি
21. একটি সমবাহু ত্রিভুজের পরিবৃত্তের ক্ষেত্রফল 462 বর্গ সেমি। ত্রিভুজটির প্রতিটি বাহুর দৈর্ঘ্য হিসাব করে লিখি।
মনে করি পরিবৃত্তের ব্যাসার্ধ্য r সেমি
শর্তানুযায়ী
πr2 = 462
বা, r2 = $\frac{462 \times 7}{22}$
বা, r2 = 21 X 7
বা, r = 7√3
সমবাহু ত্রিভুজের পরিবৃত্তের ক্ষেত্রে আমরা জানি
উচ্চতা $\times \frac{2}{3}$ = ব্যাসার্ধ্য
উচ্চতা = $\frac{2}{3} \times 7\sqrt{3} = \frac{21\sqrt{3}}{2}$
∴ সমবাহু ত্রিভুজের উচ্চতা = $\frac{21\sqrt{3}}{2}$
শর্তানুযায়ী ,
$\frac{\sqrt{3}}{2} \times a = \frac{21\sqrt{3}}{2}$
বা, a = 21
∴ সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য = 21 সেমি
22. একটি ত্রিভুজের পরিসীমা 32 সেমি. এবং ত্রিভুজটির অন্তবৃত্তের ক্ষেত্রফল 38.5 বর্গ সেমি.। ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।
ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রফল 38.5 বর্গসেমি
মনে করি অন্তর্বৃত্তের ব্যাসার্ধ্য r সেমি
$\pi r^2$ = 38.5
বা, $r^2 = \frac{38.5 \times 7}{22}$
বা, $r^2 = \frac{3.5 \times 7}{2}$
বা, $r^2 = \frac{7 \times 35}{2 \times 10}$
বা, r = $\frac{7}{2}$
আমরা জানি অন্তর্বৃত্তের ক্ষেত্রে,
∴ উচ্চতা $\times \frac{1}{3}$ = ব্যাসার্ধ্য
উচ্চতা = $ 3 \times \frac{7}{2}$
মনে করি ত্রিভুজটির বাহুর দৈর্ঘ্য a সেমি
$\frac{\sqrt{3}}{2} \times a = \frac{21}{2}$
বা, a = $\frac{21}{\sqrt{3}}$
বা, a = $\frac{21\sqrt{3}}{3}$ = 7√3
∴ ত্রিভুজটির ক্ষেত্রফল = $\frac{sqrt{3}{4} \times 7\sqrt{3} \times 7\sqrt{3}$ = 63.6 বর্গসেমি
23. 20 সেমি., 15 সেমি. এবং 25 সেমি. বাহুবিশিষ্ট ত্রিভুজের অন্তবৃত্ত ও পরিবৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি। অন্তবৃত্ত ও পরিবৃত্তের ক্ষেত্রফল হিসাব করে নির্ণয় করি।
ত্রিভুজের অর্ধপরিসীমা (S) = $\frac{20+15+25}{2}$ = 30 সেমি
∴ ত্রিভুজটির ক্ষেত্রফল = $\sqrt{30 \times (30-20) (30-15) (30-25)}$ বর্গসেমি
= $\sqrt{30 \times 10 \times 15 \times 5 }$
= $\sqrt{5 \times 3\times 2\times 5\times 2 \times 5 \times 3 \times 5}$
= 150 বর্গসেমি
মনে করি 20 সেমি বাহুর উপর বিপরীত শীর্ষবিন্দু হতে লম্বের দুরুত্ব = a সেমি
শর্তানুযায়ী,
$\frac{1}{2} \times 20 \times$ a = 150
বা, a = 15
∴ অন্তর্বৃত্তের ব্যাসার্ধ্য = $\frac{a}{3} = \frac{15}{3}$ = 5 সেমি
∴ অন্তর্বৃত্তের ক্ষেত্রফল = $\frac{22}{7} \times 5^2 = 78\frac{4}{7}$ বর্গসেমি
আমরা জানি বিষমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র বৃহত্তম বাহুর মধ্যস্থিত অবস্থিত
পরিবৃত্তের ব্যাসার্ধ্য = $\frac{25}{2}$ = 12.5 সেমি
∴ পরিবৃত্তের ক্ষেত্রফল = $\frac{22}{7} \times \frac{25}{2} \times \frac{25}{2} = 491\frac{1}{14}$
ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রফল 78$\frac{4}{7}$ এবং পরিবৃত্তের ক্ষেত্রফল $491\frac{1}{14}$
24. জয়া একটি বর্গক্ষেত্রের অন্তর্বৃত্ত অঙ্কন করল। ওই বৃত্তটি আবার একটি সমবাহু ত্রিভুজের পরিবৃত্ত যার প্রত্যেক বাহুর দৈর্ঘ্য সেমি.। বর্গক্ষেত্রটির একটি কর্ণের দৈর্ঘ্য হিসাব করে লিখি।
সমবাহুর ত্রিভুজটির বাহুর দৈর্ঘ্য = $4\sqrt{3}$
∴ সমবাহুর ত্রিভুজটির উচ্চতা = $\frac{\sqrt{3}}{2} \times$ বাহু
= $\frac{\sqrt{3}}{2} \times 4\sqrt{3}$ = 6 সেমি
∴ সমবাহুর ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ্য = 6 $\times \frac{2}{3}$ = 4 সেমি
∴ বৃত্তটির ব্যাস = 2 $\times$ 4 = 8 সেমি
∴ বৃত্তটির ব্যাসের দৈর্ঘ্য = বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = 8 সেমি
∴ বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য = $\sqrt{2} \times 8 = 8\sqrt{2}$ সেমি
25. সুমিত একটি তারকে দুটি সমান অংশে কাটল। একটি অংশকে বর্গাকারে ও অপর অংশটিকে বৃত্তাকারে বাঁকাল। বৃত্তাকার তারটি বর্গাকার তারটির থেকে 33 বর্গসেমি. বেশি জায়গা নিলে তারটির প্রকৃত দৈর্ঘ্য হিসাব করে লিখি।
মনে করি তারটির দৈর্ঘ্য a সেমি
∴ বর্গাকার তারটির দৈর্ঘ্য = বৃত্তাকার তারটির দৈর্ঘ্য = $\frac{a}{2}$ সেমি
মনে করি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = d সেমি এবং বৃত্তটির ব্যাসার্ধ্য r সেমি
শর্তানুযায়ী
4d = $\frac{a}{2}$
বা, d = $\frac{a}{8}$
এবং $ 2 \times \frac{22}{7} \times r = \frac{a}{2}$
বা, r = $\frac{7a}{88}$
শর্তানুযায়ী ,
$\frac{22}{7} \times (\frac{7a}{88})^2 – (\frac{a}{2})^2$ = 33
বা, $\frac{22 \times 7 \times 7}{7 \times 88 \times 88} a^2 – \frac{a^2}{64}$ = 33
বা, $\frac{a^2}{32} (\frac{7}{11} – \frac{1}{2})$ = 33
বা, $\frac{a^2}{32} (\frac{14-11}{22})$ = 33
বা, $a^2 = \frac{33 \times 32 \times 22}{3}$
বা, $a^2 = 11 \times 11 \times 64$
বা, a = 11 X 8
বা, a = 88
তারটির প্রকৃত দৈর্ঘ্য 88 সেমি
