Koshe Dekhi 16 Class 9 বৃত্তের পরিধি

প্রিয় ছাত্র ছাত্রী তোমাদের প্রয়োজনমত সব প্রশ্নের উত্তর দেওয়ার জন্য আমরা এই estudypoint.com ওয়েবসাইট বানিয়েছি। আজকের এই পোস্টে আমরা মধ্য শিক্ষা পর্ষদের নবম শ্রেণীর বৃত্তের পরিধি: কষে দেখি 16 class 9 এই চ্যাপ্টারের গণিতের সম্পূর্ণ উত্তর দিয়েছি।

যদি তোমাদের আরো ও গণিতের সমাধানের প্রয়োজন হয় তাহলে আমাদের এই ওয়েবসাইটের কমেন্ট বক্সে লিখে জানাবে। আমরা চেষ্টা করবো যত তাড়াতাড়ি তোমাদের প্রশ্নের উত্তর দিতে পারি।

Koshe Dekhi 16 Class 9

---

1. নীচের ছবিগুলির পরিসীমা হিসাব করে লিখি –

(i)

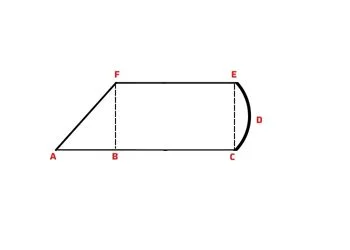
AC = 8 মি ; EF = BC= 4 মি

AB = (8 – 5) = 3 মিটার

BF = CE = 4 মিটার

∴ CDE অর্ধবৃত্তের ব্যাসার্ধ r = $\frac{CE}{2}=\frac{4}{2}=2$

∴ CDE অর্ধবৃত্তের পরিধি = $\pi r=\frac{22}{7}\times 2=\frac{44}{7}$

AF = $\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$

∴ ABCDEF এর পরিসীমা = ( 8 + 44/7 + 5 +5) = (18 + $\frac{44}{7})$

= $\frac{126+44}{7}=\frac{170}{7}=24\frac{2}{7}$ মিটার

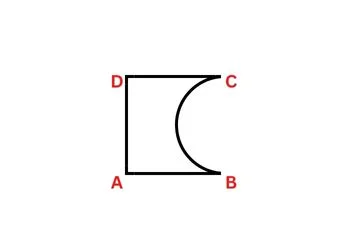
AB = AD = DC = 14 সেমি 

∴ BC বৃত্তচাপের পরিধি = $\frac{22}{7}\times 7$ = 22 মিটার

ABCD এর পরিসীমা = (14 + 14 + 22 + 14) = 64 মিটার

---

2. 35 মিটার দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্তাকার তারের রিং তৈরি করতে কত লম্বা তার নেব হিসাব করে লিখি।

তারের রিংটির ব্যাসার্ধ্য = 35 মিটার

∴ পরিধি = $(2\times \frac{22}{7}\times 35)$ = 220 মিটার

সুতরাং তারের রিংটি তৈরী করতে 220 মিটার লম্বা তার লাগবে

---

3. একটি ট্রেনের চাকার ব্যাসার্ধের দৈর্ঘ্য 0.35 মিটার। 1 মিনিটে চাকাটি 450 বার ঘুরলে ট্রেনটির গতিবেগ ঘণ্টায় কত কিমি হিসাব করে লিখি।

ট্রেনের চাকার ব্যাসার্ধ = 0.35 মিটার

∴ ট্রেনের চাকার পরিধি = $(2\times \frac{22}{7}\times 0.35)$ = 2.2 মিটার

∴ চাকাটি 1 মিনিটে যায় (2.2 X 450) মিটার = 990 মিটার

∴ চাকাটি 60 মিনিটে যায় (990 X 60) = 59400 মিটার = 59.4 কিমি

ট্রেনটির ঘন্টায় গতিবেগ 59.4 মিটার

---

4. আমােদপুর গ্রামের একটি বৃত্তাকার মাঠের ব্যাসার্ধের দৈর্ঘ্য 280 মিটার। চৈতালি প্রতি ঘণ্টায় 5.5 কিমি. বেগে হেঁটে মাঠটি পরিক্রমা করতে চায়। হিসাব করে দেখি মাঠটি একবার প্রদক্ষিণ করতে চৈতালির কত সময় লাগবে ?

বৃত্তাকার মাঠটির ব্যসার্ধ = 280 মিটার

∴ বৃত্তাকার মাঠটির পরিধি = $(2\times \frac{22}{7}\times 280)$ = 1760 মিটার = 1.76 কিমি

চৈতলি 5.5 কিমি যায় 60 মিনিটে

চৈতালি 1 কিমি যায় $\frac{60}{5.5}$ মিনিটে

চৈতালি 1.76 কিমি যায় $\frac{60\times 1.76}{5.5}=\frac{105.6}{5.5}$ = 19 মিনিট 12 সেকেন্ড

---

5. তথাগত একটি তামার তার আয়তাকারে বেঁকিয়েছে যার দৈর্ঘ্য 18 সেমি. এবং প্রস্থ 15 সেমি.। আমি এই তামার তারটি বেঁকিয়ে বৃত্ত তৈরি করলাম৷ হিসাব করে এই বৃত্তাকার তামার তারটির ব্যাসার্ধের দৈর্ঘ্য লিখি।

আয়তাকার তামার তারটির দৈর্ঘ্য = 18 সেমি এবং প্রস্থ = 15 সেমি

আয়তাকার তামার তারটির পরিসীমা = 2 (18 + 15) = 66 মিটার

তামার তারটি বেকিয়ে বৃত্ত তৈরী করা হলে বৃত্তটির পরিধি 66 মিটার

মনে করি বৃত্তাকার তারটির ব্যসার্ধ r মিটার

$2\times \frac{22}{7}\times r$ = 66

বা, r = $\frac{66\times 7}{2\times 22}=\frac{21}{2}=10.5$

বৃত্তাকার তামার তারটির ব্যসার্ধের দৈর্ঘ্য 10.5 মিটার

---

6. একটি অর্ধবৃত্তাকার মাঠের পরিসীমা 108 মিটার হলে মাঠের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

মনে করি অর্ধবৃত্তাকার মাঠটির ব্যসার্ধ r মিটার

শর্তানুযায়ী,

πr + 2r = 108

বা, r $(\frac{22}{7}+2)$ = 108

বা, r $(\frac{22+14}{7})$ = 108

বা, r = $\frac{108+7}{36}$

বা, r = 3 X 7 = 21

মাঠটির ব্যাসের দৈর্ঘ্য = (21 X 2) = 42 মিটার

---

7. একটি চাকার পরিধি ও ব্যাসের দৈর্ঘ্যের অন্তর 75 সেমি. হলে, ওই চাকার ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।

মনে করি চাকাটির ব্যসার্ধ = r সেমি

চাকাটির ব্যাস = 2r সেমি

চাকাটির পরিধি = 2πr সেমি

শর্তানুযায়ী

2πr – 2r = 75

বা, 2r (π – 1) 75

বা, 2r ($\frac{22}{7}$ -1) = 75

বা, 2r $(\frac{22-7}{7})$ = 75

বা, r = $\frac{75\times 7}{15\times 2}=\frac{35}{2}$ = 17.5

ওই চাকার ব্যসার্ধ 17.5 সেমি

---

8. 28 মিটার দৈর্ঘ্যের ব্যাসবিশিষ্ট বৃত্তাকার ট্র্যাকে পূজা ও জাকির একই জায়গা থেকে একই সময়ে প্রতিযােগিতা শুরু করে। পূজা যখন 4 পাক ঘুরে প্রতিযােগিতা শেষ করে জাকির তখন একপাক পিছনে থাকে। প্রতিযােগিতাটি কত মিটারের ছিল এবং পূজা জাকিরকে কত মিটারে পরাজিত করেছে হিসাব করে লিখি।

সমাধান:

প্রদত্ত, বৃত্তাকার ট্র্যাকের ব্যাস = 28 মিটার

ট্রাকটির ব্যসার্ধ দৈর্ঘ্য = $\frac{28}{2}$ = 14 মিটার

ট্রাকটির পরিধি = 2 $\times \frac{22}{7}\times 14$

= 88 মিটার

পূজা 4 পাক ঘুরে প্রতিযােগিতা শেষ করে,

সুতরাং, প্রতিযােগিতাটি ছিল = 88 মিটার × 4 পাক

= 352 মিটারের

---

9. আমাদের পাড়ার একটি পাতকুয়াের পরিধি 440 সেমি.। এই পাতকুয়াের চারধারে সমান চওড়া একটি পাথরের পাড় আছে। যদি বেধসমেত পাতকুয়াের পরিধি 616 সেমি. হয় তবে পাথরের পাড় কত চওড়া হিসাব করে লিখি।

সমাধান:

পাতকুয়ার পরিধি = 440 সেমি

পাতকুয়ার ব্যাসার্ধ = $\frac{400}{2\pi }=\frac{440\times 7}{2\times 22}$ = 70 সেমি

বেধসমেত পাতকুয়ার পরিধি 616 সেমি

বেধ্সমেত পাতকুয়ার পরিধি = $\frac{616}{2\pi }=\frac{616\times 7}{2\times 22}$ = 98 সেমি

পাথরের পার (98 – 70) = 28 সেমি চওড়া

---

10. গ্রামের নিয়ামতচাচা একটি মােটরের চাকার সঙ্গে বেল্ট দিয়ে একটি মেশিনের চাকা যুক্ত করেছেন। মােটরের চাকার ব্যাসের দৈর্ঘ্য 14 সেমি. এবং মেশিনের চাকার ব্যাসের দৈর্ঘ্য 94.5 সেমি.। মােটরের চাকা যদি প্রতি সেকেন্ডে 27 বার ঘােরে, তবে মেশিনের চাকা ঘণ্টায় কতবার ঘুরবে হিসাব করে লিখি।

সমাধান:

মোটরের চাকার ব্যাসের দৈর্ঘ্য = 14 সেমি

মোটরের চাকার পরিধি = $(\frac{22}{7}\times 14)$ = 14 সেমি

মেশিনের চাকার ব্যাসের দৈঘ্য = 94.5 সেমি

∴ মেশিনের চাকার পরিধি = $(\frac{22}{7}\times 94.5)$ = 297 সেমি

মোটরের চাকার পরিধি 44 সেমি

∴ মোটরের চাকা প্রতি সেকেন্ডে অতিক্রম করে = (44 $\times$ 27) = 1188 সেমি

∴ মেশিনের চাকা 1 সেকেন্ডে ঘোরে $\frac{1188}{297}$ = 4 বার

∴ মেশিনের চাকা 3600 সেকেন্ডে ঘোরে = (4 $\times$ 3600) = 14400 বার

মেশিনের চাকা ঘন্টা 14400 বার ঘুরবে

---

11. আমাদের ক্লাব ঘরের ঘড়িটির ঘণ্টার কাঁটা ও মিনিটের কাঁটার দৈর্ঘ্য যথাক্রমে 8.4 সেমি. ও 14 সেমি.। একদিনে প্রতিটি কাঁটা কতটা পথ অতিক্রম করবে হিসাব করে লিখি।

ঘড়িটির ঘণ্টার কাঁটার পরিধি = 2πr = $2\times \frac{22}{7}\times 8.4$ = 52.8 সেমি

ঘণ্টার কাঁটা 12 ঘন্টায় 1 বার পরিক্রমা করে অর্থাৎ একদিনে অর্থাৎ, 24 ঘন্টায় কাঁটাটি 2 বার সমগ্র ঘড়িটি অতিক্রম করে। 

∴ একদিনে ঘন্টার কাঁটা মোট পথ অতিক্রম করে = 2 × 52.8 সেমি.

= 105.6 সেমি.

ঘড়িটির মিনিটের কাঁটার পরিধি = 2πR = $2\times \frac{22}{7}\times 14$ = 88 সেমি.

মিনিটের কাঁটা 1 ঘন্টায় 1 বার পরিক্রমা করে। 

একদিনে অর্থাৎ, 24 ঘন্টায় কাঁটাটি 24 বার সমগ্র ঘড়িটি অতিক্রম করে। 

∴ একদিনে মিনিটের কাঁটা মোট পথ অতিক্রম করে = 24 × 88 সেমি.

= 2112 সেমি.

একদিনে ঘন্টার কাঁটা 105.6 সেমি এবং মিনিটের কাঁটা 2112 সেমি অতিক্রম করবে

---

12. আমি ও বন্ধু মিহির দুটি বৃত্ত এঁকেছি যাদের ব্যাসের দৈর্ঘ্যের অনুপাত [] : [] । হিসাব করে দেখছি আমাদের বৃত্তের পরিধির অনুপাত হয় [] : [] ।

সমাধান;

বৃত্ত দুটির ব্যাসের অনুপাত 2 : 3

মনে করি বৃত্ত দুটির ব্যাস 2r এবং 3r

বৃত্তদুটির পরিধির অনুপাত = $2\pi \times \frac{2r}{2}:2\pi \frac{3r}{2}$ = 2 : 3

আমাদের বৃত্তের পরিধির অনুপাত 2 : 3

---

13. রহিমের একটি বৃত্তাকার মাঠের পুরোটা একবার দৌড়াতে যে সময় লাগে ব্যাস বরাবর একপ্রান্ত থেকে আর একপ্রান্তে যেতে 40 সেকেন্ড কম সময়। লাগে। রহিমের গতিবেগ 90 মিটার প্রতি মিনিট হলে, মাঠের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

রহিমের গতিবেগ মিনিটে 90 মিটার

রহিম 60 সেকেন্ডে যায় 90 মিটার

রহিম 1 সেকেন্ডে যায় $\frac{90}{60}$ মিটার

রহিম 40 সেকেন্ডে যায় $\frac{90\times 40}{60}$ = 60 মিটার

মনে করি বৃত্তাকার মাঠটির ব্যাসার্ধ r মিটার

শর্তানুযায়ী,

2πr – 2r = 60

বা, 2r (π – 1) = 60

বা, 2r$(\frac{22}{7}–1)$ = 60

বা, 2r $\times (\frac{22–7}{7})$ = 60

বা, 2r = $\frac{60\times 7}{15}$

বা, 2r = 28

মাঠের ব্যাসের দৈর্ঘ্য 28 মিটার

---

14. দুটি বৃত্তের পরিধির অনুপাত 2 : 3 এবং তাদের ব্যাসার্ধের দৈর্ঘ্যের অন্তর 2 সেমি। বৃত্ত দুটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধান,

ধরি, ছোট বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি এবং বড় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য (r + 2) সেমি। 

ছোট বৃত্তের পরিধি = 2πr সেমি এবং বড় বৃত্তের পরিধি = 2π (r + 2) সেমি

শর্তানুযায়ী

$\frac{2\pi r}{2\pi (r+2)}=\frac{2}{3}$

বা, $\frac{r}{(r+2)}=\frac{2}{3}$

বা, 3r = 2r + 4

বা, 3r – 2r = 4

বা, r = 4

ছোট বৃত্তের ব্যাস = 2 × ছোট বৃত্তের ব্যাসার্ধ

= 2 × 4 = 8 সেমি

বড় বৃত্তের ব্যাস = 2 × বড় বৃত্তের ব্যাসার্ধ

= 2 × (4 + 2) = 2 × 6 = 12 সেমি

---

15. 196 বর্গ সেমি. ক্ষেত্রফলের একটি বর্গাকার পিতলের পাত থেকে চারটি সর্ববৃহৎ বৃত্তাকার পাত কেটে নেওয়া হলাে। প্রতিটি বৃত্তাকার পাতের পরিধি হিসাব করে লিখি।

সমাধান

বর্গাকার পিতলের পাতটির ক্ষেত্রফল = 196 বর্গসেমি

∴ বর্গাকার পিতলের পাতটির বাহুর দৈর্ঘ্য = $\sqrt{196}$ = 14 সেমি

14 সেমি বহু বিশিষ্ট বর্গাকার পাত থেকে যদি চারটি সর্ববৃহৎ পিতলের পাত কেটে নেওয়া হয় তাহলে প্রতিটি বৃত্তাকার পাতের ব্যাস হবে $\frac{14}{2}=7$ সেমি

∴ বৃত্তাকার পাতের ব্যাসার্ধ হবে $\frac{7}{2}$ সেমি

∴বৃত্তাকার পাতের পরিধি = $2\times \frac{22}{7}\times \frac{7}{2}$ = 22 সেমি

প্রতিটি বৃত্তাকার পাতের পরিধি 22 সেমি হবে

---

16. একটি বৃত্তাকার মাঠের বৃত্ত বরাবর একপ্রান্ত থেকে অপরপ্রান্তে যেতে নাসিফার যে সময় লাগে মাঠের ব্যাস বরাবর অতিক্রম করতে তার থেকে 45 সেকেন্ড সময় কম লাগে। নাসিফার গতিবেগ মিনিটে 80 মিটার হলে, মাঠটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

নাসিফার গতিবেগ মিনিটে 80 মিটার

নাসিফা 60 সেকেন্ডে যায় 80 মিটার

নাসিফা 1 সেকেন্ডে যায় $\frac{80}{60}$ মিটার

নাসিফা 45 সেকেন্ডে যায় $\frac{80\times 45}{60}$ = 60 মিটার

মনে করি মাঠটির ব্যসার্ধ = r মিটার

শর্তানুযায়ী

2πr – 2r = 60

বা, 2r (π – 1) = 60

বা, 2r $(\frac{22}{7}–1)$ = 60

বা, 2r $\times (\frac{22-7}{7})$ = 60

বা, 2r = $\frac{60\times 7}{15}$

বা, 2r = 28

মাঠটির ব্যাস 28 মিটার

---

17. মহিম সাইকেলে চেপে 7 মিটার 5 ডেসিমি. চওড়া একটি বৃত্তাকার পথের বাইরের ও ভিতরের ধার বরাবর সম্পূর্ণ একবার ঘুরতে যথাক্রমে 46 সেকেন্ড ও 44 সেকেন্ড নেয়। ভিতরের ধার বরাবর বৃত্তটির ব্যাসের দৈর্ঘ্য হিসাব করি।

সমাধান

বৃত্তাকার পথটির দৈর্ঘ্য 7 মিটার 5 ডেসিমি = 7.5 মিটার

বৃত্তাকার পথটির বাইরের দিক অতিক্রম করতে সময় লাগে 46 সেকেন্ড

বৃত্তাকার পথটির ভিতরের দিক অতিক্রম করতে সময় লাগে 44 সেকেন্ড

মহিম (46 – 44) সেকেন্ড = 2 সেকেন্ড যায় 7.5 মিটার

মহিম 1 সেকেন্ডে যায় $\frac{7.5}{2}$ মিটার

মহিম 44 সেকেন্ডে যায় $\frac{7.5\times 44}{2}$ = 7.5 × 22 = 165 মিটার

বৃত্তাকার পথটির ভিতরের ব্যাসার্ধ = 165 মিটার

বৃত্তাকার পথটির ভিতরে ব্যাস = (165 × 2) = 330 মিটার

---

18. একজন সাইকেল আরােহীর একটি বৃত্তাকার পথে বাইরের ও ভিতরের ধার বরাবর সম্পূর্ণ একবার ঘুরতে সময়ের অনুপাত 20 : 19; যদি পথটি 5 মিটার চওড়া হয়, তবে ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য লিখি।

সমাধান

মনে করি সাইকেল আরোহী বাইরের দিক ঘুরতে সময় লাগে 20x সেকেন্ড

এবং সাইকেল আরোহী ভিতরের দিক ঘুরতে সময় লাগে 19x সেকেন্ড

(20x – 19x) সেকন্ডে = x সেকেন্ডে যায় 5 মিটার

19x সেকেন্ডে যায় $\frac{5\times 19x}{x}$ = 95 মিটার

বৃত্তটির ভিতরে ব্যাসার্ধ 95 মিটার

বৃত্তটির ভিতরের ব্যাস (95 × 2) = 190 মিটার