In mathematics, the phrase “antilog” refers to the inverse of the logarithm. Logarithms and antilogs are closely related mathematical concepts that are used to solve exponential equations and conduct computations requiring extremely large or small integers.
It finds applications in various fields, particularly when dealing with exponential growth, signal processing, and working with large or small quantities in scientific notation.
The antilogarithm serves as a powerful tool for recovering original values from their logarithmic representation, particularly in scientific and engineering fields where logarithms are frequently used. While it has several practical applications, it also comes with limitations related to precision, complexity, and applicability in non-exponential scenarios.
In this article, we have discussed the definition, method of antilog, Finding steps of antilog, and merits and demerits of antilog. Also, detailed examples of antilog will be discussed.
What are Antilogs in Math?
In mathematics, the term “antilog” refers to the inverse operation of the logarithm. Specifically, if you know the logarithm of a number, the antilog will give you back the original number.
Let
x =log a, then antilog (x)=a
The word antilog is only another word for results or numbers. Let’s suppose 23=8, the results are “8” is called antilog
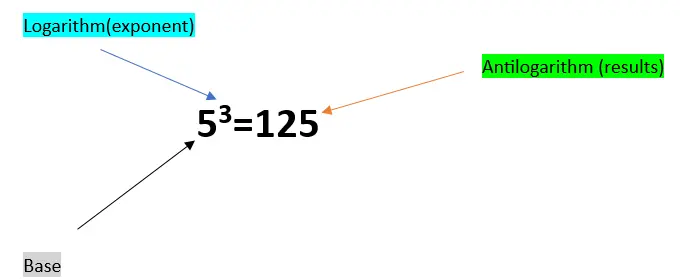
Steps For Finding Antilogarithmic
To find the antilogarithm (antilog) of a given number, you need to know the base of the logarithm. The steps of antilog are discussed below
Step 1: identify the number
Let x be the given number
Step 2: Find the base of the log function
Determine the base of the logarithm of the function whose antilog you want to determine. Assume you have a logarithm in the form of log base b of x, and the base is b.
Step 3: Use the antilogarithm formula.
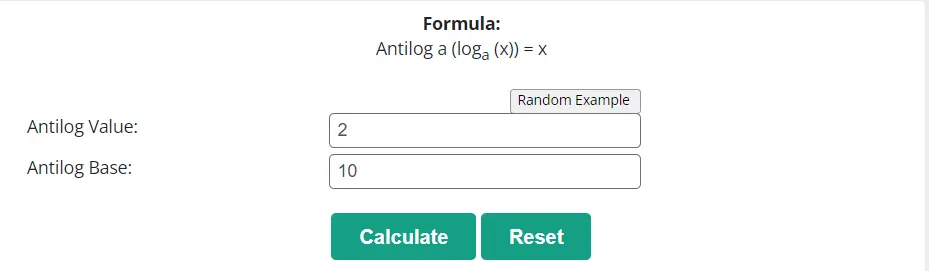
The antilogarithm formula is given as follows:
Antilog (base b) of x = bx
Step 4: Calculate the antilogarithm.
To find the antilogarithm raise the base “b” to the power of the given number “x”.
An antilog calculator can be usedto calculate the value of an antilogarithm by following the provided steps.
Merits and demerits of antilog
The term “antilog” refers to the process of determining the original value from a given logarithm. While the antilogarithm can be a useful mathematical tool, it also offers advantages and disadvantages depending on the context.
| Number | Name | Merits | Name | Demerits |
|---|---|---|---|---|
| 1 | Inverse of Logarithm | It allows us to recover the original value from its logarithmic representation, making it valuable in solving exponential equations and problems involving exponential growth or decay. | Precision and Rounding Errors | In some cases, when calculating the antilog of a logarithmic value, there might be rounding errors or loss of precision, especially when using approximate values of logarithms. |
| 2 | Exponential Computations | Antilog is essential for performing computations involving very large or small numbers that are expressed in logarithmic form. It helps convert logarithmically scaled data back to its original linear scale. | Limited Applicability | The concept of antilog is most useful in contexts where logarithms are frequently used, such as scientific and engineering fields. In everyday arithmetic or basic mathematics, antilog might not have much significance. |
| 3 | Application in Scientific Notation | When using a standard form (scientific notation) to represent very large or small numbers, antilog is used to convert the exponent back to the original number, making it easier to understand and work with such values. | Complex Computations | In certain situations, finding the antilogarithm of extremely large or small logarithmic values can involve complex computations, which may be challenging without the aid of a calculator or software. |
| 4 | Signal Processing and Engineering | In signal processing and engineering applications, antilog is commonly used to convert logarithmically scaled data, such as dB (decibel) values, back to their original linear values. | Ambiguity | If the base of the logarithm is not explicitly provided, finding the antilogarithm is not possible without additional information. |
| 5 | Limited Use in Non-Exponential Scenarios | Antilog is specifically applicable to exponential relationships. In other types of mathematical equations, the concept of antilog might not be directly relevant. |
Example section
Example 1:
Determine the antilogarithmic for base 8 and the value of log is 2.
Answer:
Given data
Antilog log=2
Base=8
We can find Antilog’s step-by-step process
Step 1:
Formula for antilog
x= Antilog a(loga(X)) (i)
A=2, b=8
Step 2:
Put the given value in the formula
Log8(x)=2
Step 3:
Substitute values in equation (i)
x= antilog 8(2)
x=82
x=64
Example 2:
log₁₀ (1000) = 3.
Antilog=?
Step 1:
The base of the given function is 10
Step 2:
Value of exponent=3.
Step 3:
Raise the base and exponent = 103 = 1000
Step 4:
Antilog= 1000.
So, the antilogarithm of log₁₀ (1000) to the base 10 is 1000.
FAQs regarding antilogarithmic
Question number 1:
What are some practical applications of antilogs?
Answer:
Antilogs find applications in many fields, such as engineering,finance, physics, and biology. Also, other applications like decibel Conversions, pH and concentration, exponential Growth and Decay, Geophysics and Seismology, Signal Processing, Photography and Exposure, and biomedical Data Analysis in all term antilog play an important role in converting logarithmic to back its linear form making it easier for scientists, researchers, and professionals to interpret and work with data in various fields.
They are useful for reverse calculations involving logarithmic scales, exponential growth or decay, and converting logarithmic data back to its original form.
Question number 2:
Can I calculate an antilog using a calculator?
Answer:
Yes, modern calculators, including scientific calculators, have built-in functions to calculate antilogs. Typically, you can find an “antilog” or “10x” button on the calculator to perform these calculations easily.
Question number 3:
Can antilogs be negative or complex?
Answer:
Antilogs can be negative or complex when the logarithmic value used to calculate them is negative or complex, respectively. The base used in the antilog doesn’t affect whether the result will be positive, negative, or complex.
Conclusion
In this article, we discuss the definition, methods, and steps for finding the antilog, along with its merits and demerits. Detailed examples are also provided. After reading this article, readers will be well-equipped to understand and explain the concept of antilog.
