প্রিয় ছাত্র ছাত্রী তোমাদের প্রয়োজনমত সব প্রশ্নের উত্তর দেওয়ার জন্য আমরা এই estudypoint ওয়েবসাইট বানিয়েছি। আজকের এই পোস্টে আমরা মধ্য শিক্ষা পর্ষদের নবম শ্রেণীর গণিত কষে দেখি 2 সূচকের নিয়মাবলী: Kose Dekhi 2 Class 9 এই চ্যাপ্টারের গণিতের সম্পূর্ণ উত্তর দিয়েছি। যদি তোমাদের আরো ও গণিতের সমাধানের প্রয়োজন হয় তাহলে আমাদের এই ওয়েবসাইটের কমেন্ট বক্সে লিখে জানাবে। আমরা চেষ্টা করবো যত তাড়াতাড়ি তোমাদের প্রশ্নের উত্তর দিতে পারি।
Kose Dekhi 2 Class 9
1. মান নির্ণয় করো :
(i) $ \left( \sqrt[5](8) \right) ^ \frac{5}{2} \times \left( 16 \right) ^ \frac{-3}{2}$
$= (8^\frac{1}{5})^\frac{5}{2}\times(2^4)^\frac{-3}{2}$
$= 8^{[\frac{1}{5}\times\frac{5}{2}]}\times 2^{[4\times(\frac{-3}{2})]}$
$= 8^{[\frac{1}{5}\times\frac{5}{2}]}\times 2^{[4\times(\frac{-3}{2})]}$
$=8^\frac{1}{2} \times 2^{-3}$
$=(2^3)^\frac{1}{2} \times 2^{-3}$
$=2^{[\frac{3}{2} -3]}$
$=2^\frac{3-2}{2}$
$=2^\frac{3}{2}$
$(ii)[(125)^-2 \times (16)^\frac{-3}{2}]^\frac{-1}{6}$
$=[(15^3)^-2 \times(2^4)^\frac{-3}{2}]^\frac{1}{6}$
$=(5^{-6})^\frac{-1}{6} \times [2^{[4\times(\frac{-3}{2})]}]^\frac{-1}{6}$
$=5^{[(-6)\times(-\frac{1}{6})]} \times (2^{-6})^\frac{-1}{6}$
$=5\times2$
$=10$
$(iii) 4^\frac{1}{3}\times[2^\frac{1}{3}\times 3^\frac{1}{2}\div9^\frac{1}{4}$
$=\frac{2^\frac{2}{3}\times2^\frac{1}{3}\times3 ^\frac{1}{2}}{(3^2)^\frac{1}{4}}$
$=\frac{2^\frac{2}{3}\times 2^\frac{1}{3}\times 3^\frac{1}{2}}{3^\frac{1}{2}}$
=$2^{\frac{2}{3}+\frac{1}{3}}$
$=2^\frac{3}{3}$
= 2
2. সরল করো :
$(i) (8a^3 \div 27x^-3)^\frac{2}{3} \times (64a^3 \div 27x^-3)^-\frac{2}{3}$
$=(8a^3\times\frac{1}{27x^-3})^\frac{2}{3} \times (64a^3\times \frac{1}{27x^-3})^\frac{-2}{3}$
$=(\frac{8a^3 x^3}{27}) \times (\frac{64a^3x^3}{27})^\frac{-2}{3}$
$=(\frac{2ax}{3})^3 \times (\frac{4ax}{3})^{3\times(-11)}$
$= (\frac{2ax}{3})^3 \times (\frac{4ax}{3})^{-2}$
= $\frac{2^2(ax)^{2-2} \times 4^{-2}}{3^{2-2}}$
$=2^2 \times 2^{-4}$
$=2^{2-4}$
$=2^{-2}$
$=\frac{1}{4}$
$(ii)\quad {(x^{-5})^\frac{2}{3}}^{-\frac{3}{10}}$
$=[x^{-\frac{10}{3}}]^{-\frac{3}{10}}$
$=x^{-\frac{10}{3}\times -\frac{3}{10}}$
$=x^1$
$=x$
$(iii) [\{{{(2^{-1})^{-1}}}\}^{-1}]^{-1}$
$=[\{(\frac{1}{2})^{-1}\}^{-1}]^{-1}$
$=[\{2\}^{-1}]^{-1}$
$=[\frac{1}{2}]^{-1}$
=2
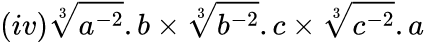
$=a^{- \frac{2}{3}} \times b^ {- \frac{2}{3}} \times c^ {- \frac{2}{3}} \times abc$
$=a^{1 – \frac{2}{3}}\times b^{1-\frac{2}{3}}\times c^{1-\frac{2}{3}}$
$=a^\frac{1}{3} \times b^\frac{1}{3} \times c^\frac{1}{3}$
$=(abc)^\frac{1}{3}$
(v) $\left(\frac{4^{m+\frac{1}{4}}\times\sqrt{2\times2^m}}{2.\sqrt{2^{-m}}}\right)^{\frac{1}{m}}$
$=\left(\frac{2^{2(m+\frac{1}{4})} \times 2^{\frac{m+1}{2}}}{2^1\times2^{\frac{-m}{2}}}\right)^\frac{1}{m}$
$=\left(\frac{2^{2m+\frac{1}{2}+\frac{m}{2}+\frac{1}{2}}}{2^{1-\frac{m}{2}}}\right)^\frac{1}{m}$
$=\left(2^{2m+\frac{1}{2}+\frac{m}{2}+\frac{1}{2}+\frac{m}{2}} \right)^{\frac{1}{m}}$
$=\left(2^{3m}\right)^{\frac{1}{m}}$
$=2^3$
=8
(vi) $9^{-3} \times \frac{16^\frac{-1}{4}}{6^{-2}}\times \left(\frac{1}{27}\right)^{\frac{-4}{3}}$
=$\frac{3^{-6} \times 2^{4\times\frac{-1}{4}}}{3^{-2}\times2^{-2}} \times 3^{-3 \times \frac{-4}{3}}$
$=3^{-6+2} \times 2^{-1+2} \times 3^{4}$
$=3^{-4} \times 3^{4} \times 2^{1}$
$=3^{-4+4}\times 2^1$
=2
$(vii) (\frac{x^a}{x^b})^{a^2+ab+b^2} \times (\frac{x^b} {x^c})^{b^2+bc+c^2} \times (\frac{x^c}{x^a})^{c^2+ca+a^2}$
$=x^{(a-b) (a^2+ab+b^2} \times x^{(b-c)(b^2+bc+c^2)} \times x^{(c-a)(c^2+ca+c^2)}$
$=x^{a^3 – b^3} \times x^{b^3-c^3} \times x^{c^3-a^3}$
$=x^{a^3-b^3+b^3-c^3+c^3-a^3}$
=x0
=1
3. মানের উর্ধ্ব ক্রমানুসারে সাজাও : (i) $5^\frac{1}{2}, 10^\frac{1}{4}, 6^\frac{1}{3}$
$5^\frac{1}{2}$ $=5^\frac{6}{12}$ $=(5^6)^\frac{1}{12}$ $=(15625)^\frac{1}{12}$
$10^\frac{1}{4}$ $=10^\frac{3}{12}$ $=(10^3)^\frac{1}{12}$ $=(1000)^\frac{1}{12}$
$6^\frac{1}{3}$ $=6^\frac{4}{12}$ $=(6^4)^\frac{1}{12}$ $=(1296)^\frac{1}{12}$
মানের উর্ধ্বক্রমানুসারে সাজিয়ে পায়, $10^\frac{1}{4}, 6^\frac{1}{3}, 5^\frac{1}{2}$
(ii) $3^\frac{1}{3}, 2^\frac{1}{2}, 8^\frac{1}{4}$
$3^\frac{1}{3}$ $=3^\frac{4}{12}$ $=(3^4)^\frac{1}{12}$ $=(81)^\frac{1}{12}$
$2^\frac{1}{2}$ $=2^\frac{6}{12}$ $=(2^6)^\frac{1}{12}$ $=(64)^\frac{1}{12}$
$8^\frac{1}{4}$ $=8^\frac{3}{12}$ $=(8^3)^\frac{1}{12}$ $=(512)^\frac{1}{12}$
মানের উর্ধ্বক্রমানুসারে সাজিয়ে পায়, $2^\frac{1}{2}, 3^\frac{1}{3},8^\frac{1}{4}$
(iiii) $2^{60}, 3^{48}, 4^{36}, 5^{24}$
$2^{60}$ $=(2^5)^{12}$ $=(32)^{12}$
$3^{48}$ $=(3^4)^{12}$ $=(81)^{12}$
$4^{36}$ $=(4^3)^{12}$ $=(64)^{12}$
$5^{24}$ $=(562)^{12}$ $=(25)^{12}$
মানের উর্ধ্বক্রমানুসারে সাজিয়ে পায়, $5^{24}, 2^{60}, 4^{36}, 3^{48}$
4. প্রমাণ করো :
(i) $(\frac{a^q}{a^r})^p \times (\frac{a^r}{a^p})^q \times (\frac{a^p}{a^q})^r =1$
বামপক্ষ $=(\frac{a^q}{a^r})^p \times (\frac{a^r}{a^p})^q \times (\frac{a^p}{a^q})^r $
$=(a^{q-r})^p \times (a^2-p)^q \times (a^{p-q})^r$
$=a^{p(q-r)} \times a^{(r-p)q} \times a^{(p-q)r}$
$=a^{pq-pr+qr-qp+rp-rq}$
=a0
=1= ডানপক্ষ (প্রমাণিত)
$(ii) (\frac{x^m}{x^n})^{m+n}\times (\frac{x^n}{x^l})^{n+l}\times (\frac{x^l}{x^m})^{l+m}=1$
বামপক্ষ = $(\frac{x^m}{x^n})^{m+n} \times (\frac{x^n}{x^l})^{n+l} \times (\frac{x^l}{x^m})^{l+m}$
$=(x^{m-n})^{m+n} \times (x^{n-l})^{n+l} \times (x^{l-m})^{l+m}$
$=x^{m^2-n^2} \times x^{n^2-l^2} \times x^{l^2-m^2}$
$=x^{m^2-n^2+n^2-l^2+l^2-m^2}$
$=x^0$
$=1=$ ডানপক্ষ (প্রমাণিত)
$(iii) (\frac{x^m}{x^n})^{m+n-l} \times (\frac{x^n}{x^l})^{n+l-m} \times (\frac{x^l}{x^m})^{l+m-n}=1$
$=x^{(m-n)(m+n-l)} \times x^{(n-l)(n+l-m)} \times x^{(l-m)(l+m-n)}$
$=x^{m^2-n^2-l(m-n)+n^2-l^2-m(n-l)+l^2-m^2-n(l-m)}$
$=x^0=1$ ডানপক্ষ (প্রমাণিত)
koshe dekhi 2 class 9
$(iv) (a^{\frac{1}{x-y}})^\frac{1}{x-z} \times (a^{\frac{1}{y-z}})^\frac{1}{y-x} \times (a^{\frac{1}{z-x}})^\frac{1}{z-y} =1$
$=a^{\frac{1}{(x-y)(x-z)}} \times a^{\frac{1}{(y-z)(y-x)}} \times a^{\frac{1}{(z-x)(z-y)}}$
$=a^{\frac{1}{(x-y)(x-z)} + \frac{1}{(y-z)(y-x)}+ \frac{1}{(z-x)(z-y)}}$
$=a^{-{\frac{1}{(x-y)(z-x)}- \frac{1}{(y-z)(x-y)} -\frac{1}{(z-x)(y-z)}}}$
$=a^{\frac{-(y-z)-(z-x)-(x-y)}{(x-y)(y-z)(z-x)}}$
$=a^{\frac{-y+z-z+x-x+y}{(x-y)(y-z)(z-x)}}$
=a0
=1 ডানপক্ষ (প্রমাণিত)
5.x+z=2y এবং b2=ac হলে দেখাই যে a y-z b z-x c x-y =1
x+z = 2y
বা, x-y = y-z
এখন , a y-z b z-x c x-y
= a y-z b z-x c y-z [∵ x-y = y-z ]
= (ac)y-z b z-x
= (b2)y-z b z-x
= b 2y-2z b z-x
= b2y-2z+z-x
= b 2y-(x+z)
= b 2y-2y [যেহেতু, x+z =2y]
= b0
=1 [ প্রমাণিত ]
6.a = xy p-1 , b = xyq-1 , c = xyr-1 হলে দেখাই যে , a q-r br-p c p-q =1
a q-r br-p c p-q
= (xy p-1 ) q-r (xy q-1)r-p (xy r-1) p-q
= x q-r y (p-1)(q-r) x r-p y (q-1)(r-p) xp-q y (r-1)(p-q)
= x q-r+r-p+p-q y (p-1)(q-r)+(q-1)(r-p) + (r-1)(p-q)
= x 0 y (pq-q-rp+r +qr-r-pq+p+rp-p-qr+q)
= x 0 y0
= 1
7. $x^\frac{1}{a} = y^\frac{1}{b}=z^\frac{1}{c}$ এবং xyz=1 হলে দেখাও যে a+b+c=0
$ x^\frac{1}{a}=y^\frac{1}{b}=z^\frac{1}{c}=k$ (k≠0, ± 1)
$x=k^a, y=k^b, z=k^c$
xyz=1
$k^{a \times k^b\times k^c}=1$
$k^{a+b+c} =k^0$
a+b+c=0 (প্রমাণিত)
8. a x = by =cz এবং abc =1 হলে দেখাই যে a+b+c=1
ধরি, $a^x=b^y=c^z=k$ (k≠0, ± 1)
$a=k^\frac{1}{x}, b=k^\frac{1}{y}, c=k^\frac{1}{z}$
abc=1
$k^\frac{1}{x} \times k^\frac{1}{y} \times k^\frac{1}{z} =1$
$ k^{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} =0$
$ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$
$\frac{yz+zx+xy}{xyz}=0$
xy+yz+zx=0 (প্রমাণিত)
9. সমাধান করিঃ
(i) 49x= 73
বা, (7)2x = (7)3
বা, 2x =3
বা, x = $\frac{3}{2}$
(ii) 2 x+2+ 2 x-1 =9
বা, 2x . 22 + 2x .2-1 =9
বা, 2x .4 + 2x $\frac{1}{2}$ =9
বা, 2x (4+ $\frac{1}{2}$)= 9
বা, 2x ($\frac{9}{2}$) = 9
বা, 2x =9✕$\frac{2}{9}$
বা, 2x = 21
বা, x =1
(iii). 2x+1 + 2x+2 =48
বা, 2x .2+2x . 22 =48
বা, 2x .2+2x .4=48
বা, 2x (2+4) =48
বা, 2x ✕ 6 =48
বা, 2x = 8
বা, 2x =23
বা, x =3
(iv) $2^{4x} \times 4^{3x-1} =\frac{4^2x}{2^3x}$
বা, $ 2^{4x} \times 2^{3x} = \frac {4^{2x}}{4^{3x-1}}$
বা, 27x = 4 2x -3x+1
বা, 27x = 4 1-x
বা, 27x = 22-2x
বা, 7x = 2-2x
বা, 7x + 2x =2
বা, 9x = 2
বা, $ x=\frac{2}{9}$
(v) 9✕ 81x = 27 2-x
বা, 32 ✕ 34x = 33(2-x)
বা, 3(2+4x) = 3(6-3x)
বা, 2+4x=6-3x
বা, 4x+3x=6-2
বা, 7x=4
বা, x=$\frac{4}{7}$
(vi) 2(5x+4) +29=210
বা, 2 (5x+4) =210 -29
বা, 2 (5x+4) =29(2-1)
বা, 2(5x+4) = 2 9
বা, 5x+4 =9
বা, 5x =9-4
বা, 5x=5
বা, x = 5/5
বা, x=1 [উত্তর]
(vii) 6 (2x+4) = 33x . 2 x+8
বা, (3✕2)(2x+4) = 3 3x . 2 x+8
বা, 3 (2x+4) . 2 (2x+4) = 3 3x . 2 x+8
বা, $\frac{3^{2x+4}}{3^{3x}} = \frac{2^{x+8}}{2^{2x+4}}$
বা, 3 (2x+4-3x) = 2 (x+8-2x-4)
বা, 3 4-x= 2 4-x
বা, $(\frac{3}{2})^{4-x}=1$
বা, $(\frac{3}{2})^{4-x}=(\frac{3}{2})^0$
বা, 4-x =0
বা, x=4 (উত্তর)

